Advanced Engineering Mathematics
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
Bartleby Related Questions Icon

Related questions

Q: Let (an)n∈ℕ be a row in ℝ such that a0=3 and an+1= (an)/2 + 2/(an) for n≥0 (a)…
A:
Q: Suppose you want to prove for all n > 0 that the property P(n) given by j(j+1) + 6. 2 + 5. 2 holds…
A:
Q: Prove that 10n +9 and 6n + 5 are relatively prime for all n E Z.
A: Two numbers are said to be prime  to each other if they  share the gcd 1. That is to say  suppose…
Q: 4.34 con't. and so a+²= ax+1-1 +29+1-2 акн - аки- = a + 2a₂²-1 = 2K-¹ + 2¹ (2-2) = 2k-1 +2k-1 H…
A:
Q: (c) Prove by induction that 3n5n² for all n € N with n ≥ 4. State clearly where you use the…
A:
Q: Make an outline for a proof by induction that 2 = n(n+1)(2n + 1) for all n E Z+. k=1
A: Note: We can solve one question at a time so kindly upload second question as another question.
Q: 3. For all positive integer n, We use indoctior For n=1 $1²=1
A:
Q: 4. Consider fn+2 fn + fn+1 (n ≥ 0), where fo = 0 and f₁ = 1. Let n E N. Prove by induction that 2n…
A:
Q: 4. Use mathematical induction to prove that Vn E Z* u {0}, []²=o(2i + 1)! > ((n + 1)!)**. n+1
A:
Q: (b) Prove by induction that for all n € N, 1 4n ´ (r − ¹) (r + ½) ¯¯ 2n +1° State clearly where you…
A: We need to prove: ∑r=1n1r-12r+12=4n2n+1 For n=1: ∑r=111r-12r+12=11-121+12=11232=43=4121+1 So, the…
Q: 3. Prove that for all n EN+, i=1 2 3² = 1 1 37
A: As per the guidelines I am answering only one question. [3] We have to prove for all n∈ℕ+…
Q: Let n = 2k with k ≥ 2. (a) Prove that pk is an element of order 2 which commutes with all elements…
A:
Q: Let n and k be integers such that (n, k) = 1. Prove that (n, n − k) = 1.
A:
Q: (1) Prove directly from the definition that: 3 n+1 →0.
A:
Q: Use induction to prove that Σmn1(2j + 1) = 3η2 3n²
A:
Q: 9. (Chapter 10, #20) Prove that for every n E N, (1+2+3+ · ..+n)2 = 13 + 23 + 33 + ...+ n³.
A: To prove the result ''∀n∈N,1+2+3+...+n2=13+23+33+...+n3'' by Mathematical induction: First prove for…
Q: Prove by Induction that Σn i=0 n³ = 0³ +1³ +2³+...+ n²³. n² (n + 1)² 4 for all n ≥ 0
A:
Q: 1. Prove that for all positive integers n, n Σj2i = (n − 1)2n+¹ +2 j=1
A: To prove that,              ∑j=1nj2j=n-12n+1+2.
Q: Prove, by induction, that Vn 2 1: (1·2·3) + (2 · 3 · 4) + + (n(n + 1)(n + 2)) =n(n+ 1)(n+ 2)(n + 3)…
A:
Q: Use a proof by induction to prove that for all n EN, 1+3+5+...+(2n-1)= 1 (2j-1) = n². 9. (9 n², that…
A:
Q: 6. The Ackermann's function is given: if m = 0 if m > 1 and n = 0 if m 2 1 and n = 1 la(m – 1,A(m,n…
A: Ackermann's function is defined as Am,n=2n ,                            m=0=0 ,…
Q: 1 Let x € (0, 1). Use induction to prove that xn for all natural numbers n ≥ 2. X
A:
Q: Prove, by induction, that for any positive integer n, n(n²-1) Σ=1 j(j - 1) = 3
A:
Q: give a combinatorial proof of the identity  P(n,k) * (n-kCm-k) = (nCm) * P(m,k) where all…
A: Detailed proof is provided in the next step.
Q: n Use induction to prove: for any integer n ≥ 1, Σ(6j – 4) = 3n² – n. j=1
A:
Q: Suppose a E Z. Prove that for any n E N, 5|2"a implies 5|a.
A:
Q: Prove by Mathematical Induction step by step: "Vn €Z+, 1! · 3! .5! . · (2n − 1)! ≥ (n!)”.” -
A:
Q: 8. (Chapter 10, #16) Prove that for every positive integer n, 2" +1< 3".
A: Using induction to prove any statement includes first proving the statement is true for n=1, then…
Q: (4) Let x € (0, 1). Use induction to prove that 1 - In X for all natural numbers n ≥ 2.
A:
Question
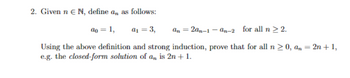
2. Given n € N, define an as follows: ao = 1, a₁ = 3, 2an-1-an-2 for all n > 2. Using the above definition and strong induction, prove that for all n ≥ 0, an = 2n + 1, e.g. the closed-form solution of an is 2n + 1. an
expand button
Transcribed Image Text:2. Given n € N, define an as follows: ao = 1, a₁ = 3, 2an-1-an-2 for all n > 2. Using the above definition and strong induction, prove that for all n ≥ 0, an = 2n + 1, e.g. the closed-form solution of an is 2n + 1. an
Expert Solution
Check Mark
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
bartleby
This is a popular solution
See solutionCheck out a sample Q&A here
Step 1: Given:
VIEW
Step 2: Proof:
VIEW
Solution
VIEW
bartleby

Trending nowThis is a popular solution!

bartleby

Step by stepSolved in 3 steps

See solution
Check out a sample Q&A here
Blurred answer
Knowledge Booster
Background pattern image
Similar questions
Recommended textbooks for you
Text book image
Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated
Text book image
Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education
Text book image
Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY
Text book image
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Text book image
Basic Technical Mathematics
Advanced Math
ISBN:9780134437705
Author:Washington
Publisher:PEARSON
Text book image
Topology
Advanced Math
ISBN:9780134689517
Author:Munkres, James R.
Publisher:Pearson,
SEE MORE TEXTBOOKS