Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Related questions
Concept explainers
Question
Solve it by using induction method:
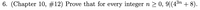
Transcribed Image Text:**Exercise: Mathematical Induction**
**Problem Statement:**
Prove that for every integer \( n \geq 0 \), \( 9 \mid (4^{3n} + 8) \).
**Solution Approach:**
To prove this statement, you may consider using the method of mathematical induction. The process involves the following steps:
1. **Base Case:** Verify the statement for the initial value \( n = 0 \).
2. **Inductive Step:** Assume the statement is true for \( n = k \), i.e., \( 9 \mid (4^{3k} + 8) \). Then, prove it for \( n = k + 1 \).
**Explanation:**
The notation \( 9 \mid (4^{3n} + 8) \) means that the expression \( 4^{3n} + 8 \) is divisible by 9 for every integer \( n \) greater than or equal to 0.
You will find that both steps of induction confirm the divisibility condition, solidifying the statement for all non-negative integers \( n \).
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 4 steps
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Similar questions
- Use bernoulli method to solvearrow_forwardSuppose you have two alloys: (A), with 7 ounces of silver per pound, (B), with 11 ounces of silver per pound, You want to make 15 pounds of an alloy with 9 ounces of silver per pound. Use Leonardo's method of double false position to solve: X₂ X² Edit Insert Formats ▾ 든든 This will require pounds of alloy B. B I Ee A Σ+ Σ Α pounds of alloy A andarrow_forwardSuppose you have two alloys: (A), with 7 ounces of silver per pound, (B), with 14 ounces of silver per pound, You want to make 15 pounds of an alloy with 11 ounces of silver per pound. Use Leonardo's method of double false position to solve:arrow_forward
- Moshiur can mow a lawn in m hours. Caroline, Moshiur’s younger sister, can mow thesame lawn in c hours. (i) Determine how long it takes for the two siblings to mow the lawn together. Use theformula(ii) How long does it take for Moshiur to mow the lawn himself, if the total time it takes forthe lawn is 1.5 hours and Caroline takes four hours longer than Moshiur?arrow_forwardSolve: logs (a) = a = Ounrtion Uoln: Gvidonarrow_forwardSolve the following DE, using Separable method.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
- Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY 
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education
Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,