Question
PLEASE ANSWER #14. The first page is provided for context.
![Certainly! Here is the transcription of the given text for educational purposes:
---
7. Find \( A_n \) by normalizing \( |n\rangle \). Suggestion: Compute \( \langle n|n\rangle \) for \( n = 0,1,2,3 \) then find the pattern. Use the identity \( \langle \hat{Q} f | g \rangle = \langle f | \hat{Q}^\dagger | g \rangle \) for \( \hat{Q} = \hat{a}^\dagger \).
8. Show that \( |n\rangle \) are the eigenvectors of \( \hat{H} \), i.e.,
\[
\hat{H} |n\rangle = E_n |n\rangle \tag{7}
\]
is satisfied. Find the energy eigenvalue \( E_n \). Knowing that \( \hat{H} \) is an observable, what can you tell about \( \langle m | n \rangle \) for \( m \neq n \)?
9. Using your results, show that the following formula holds:
\[
\hat{a}^\dagger |n\rangle = \sqrt{n+1} |n+1\rangle \tag{8a}
\]
\[
\hat{a} |n\rangle = \sqrt{n} |n-1\rangle \tag{8b}
\]
Do this either by giving a general proof or by showing that they hold for \( n = 0,1,2,3 \).
10. Let's go back to Eq.(2). What is the SI unit of the coefficient \( \sqrt{\frac{\hbar}{2m\omega}} \)? Does it make sense to you?
11. Show that the square of position operator is
\[
\hat{x}^2 = \frac{\hbar}{2m\omega} (\hat{a}^\dagger \hat{a}^\dagger + \hat{a}^\dagger \hat{a} + \hat{a} \hat{a}^\dagger + \hat{a}\hat{a}) \tag{9}
\]
12. Compute \( \langle 0 | \hat{x} |](https://content.bartleby.com/qna-images/question/4b2dbe0f-1b57-45b1-b136-e64e5f1cae33/b8549a86-30e8-4260-933d-ee8fa1aeaadb/px4iaup_thumbnail.jpeg)
Transcribed Image Text:Certainly! Here is the transcription of the given text for educational purposes:
---
7. Find \( A_n \) by normalizing \( |n\rangle \). Suggestion: Compute \( \langle n|n\rangle \) for \( n = 0,1,2,3 \) then find the pattern. Use the identity \( \langle \hat{Q} f | g \rangle = \langle f | \hat{Q}^\dagger | g \rangle \) for \( \hat{Q} = \hat{a}^\dagger \).
8. Show that \( |n\rangle \) are the eigenvectors of \( \hat{H} \), i.e.,
\[
\hat{H} |n\rangle = E_n |n\rangle \tag{7}
\]
is satisfied. Find the energy eigenvalue \( E_n \). Knowing that \( \hat{H} \) is an observable, what can you tell about \( \langle m | n \rangle \) for \( m \neq n \)?
9. Using your results, show that the following formula holds:
\[
\hat{a}^\dagger |n\rangle = \sqrt{n+1} |n+1\rangle \tag{8a}
\]
\[
\hat{a} |n\rangle = \sqrt{n} |n-1\rangle \tag{8b}
\]
Do this either by giving a general proof or by showing that they hold for \( n = 0,1,2,3 \).
10. Let's go back to Eq.(2). What is the SI unit of the coefficient \( \sqrt{\frac{\hbar}{2m\omega}} \)? Does it make sense to you?
11. Show that the square of position operator is
\[
\hat{x}^2 = \frac{\hbar}{2m\omega} (\hat{a}^\dagger \hat{a}^\dagger + \hat{a}^\dagger \hat{a} + \hat{a} \hat{a}^\dagger + \hat{a}\hat{a}) \tag{9}
\]
12. Compute \( \langle 0 | \hat{x} |
![**The Fock Operator and Harmonic Oscillator**
The Fock operator \( \hat{a} \) is defined by:
\[
\hat{a} = \sqrt{\frac{m\omega}{2\hbar}} \left( \hat{x} + \frac{i}{m\omega} \hat{p} \right) \tag{1}
\]
where \( \hat{x} \) and \( \hat{p} \) are the position and momentum operators, respectively.
**Exercises:**
1. **Determine \( \hat{a}^\dagger \)**:
- Write down \( \hat{a}^\dagger \) in terms of \( \hat{x} \) and \( \hat{p} \).
2. **Prove the following expressions**:
- \[
\hat{x} = \sqrt{\frac{\hbar}{2m\omega}} (\hat{a}^\dagger + \hat{a}) \tag{2}
\]
- \[
\hat{p} = i \sqrt{\frac{\hbar m\omega}{2}} (\hat{a}^\dagger - \hat{a}) \tag{3}
\]
3. **Canonical Commutation Relation**:
- Show that the canonical commutation relation, \([\hat{x}, \hat{p}] = i\hbar\), yields the bosonic commutation relation,
\[
[\hat{a}, \hat{a}^\dagger] = 1. \tag{4}
\]
4. **Hamiltonian of the Simple Harmonic Oscillator (SHO)**:
- Show that the Hamiltonian,
\[
\hat{H} = \frac{\hat{p}^2}{2m} + \frac{m\omega^2\hat{x}^2}{2},
\]
is written as
\[
\hat{H} = \hbar\omega \left( \hat{N} + \frac{1}{2} \right) \tag{5}
\]
where \( \hat{N} = \hat{a}^\dagger \hat{a} \) is the number operator.
5. **Hermitian Nature of \( \hat{N} \)**:
-](https://content.bartleby.com/qna-images/question/4b2dbe0f-1b57-45b1-b136-e64e5f1cae33/b8549a86-30e8-4260-933d-ee8fa1aeaadb/04ijpeq_thumbnail.jpeg)
Transcribed Image Text:**The Fock Operator and Harmonic Oscillator**
The Fock operator \( \hat{a} \) is defined by:
\[
\hat{a} = \sqrt{\frac{m\omega}{2\hbar}} \left( \hat{x} + \frac{i}{m\omega} \hat{p} \right) \tag{1}
\]
where \( \hat{x} \) and \( \hat{p} \) are the position and momentum operators, respectively.
**Exercises:**
1. **Determine \( \hat{a}^\dagger \)**:
- Write down \( \hat{a}^\dagger \) in terms of \( \hat{x} \) and \( \hat{p} \).
2. **Prove the following expressions**:
- \[
\hat{x} = \sqrt{\frac{\hbar}{2m\omega}} (\hat{a}^\dagger + \hat{a}) \tag{2}
\]
- \[
\hat{p} = i \sqrt{\frac{\hbar m\omega}{2}} (\hat{a}^\dagger - \hat{a}) \tag{3}
\]
3. **Canonical Commutation Relation**:
- Show that the canonical commutation relation, \([\hat{x}, \hat{p}] = i\hbar\), yields the bosonic commutation relation,
\[
[\hat{a}, \hat{a}^\dagger] = 1. \tag{4}
\]
4. **Hamiltonian of the Simple Harmonic Oscillator (SHO)**:
- Show that the Hamiltonian,
\[
\hat{H} = \frac{\hat{p}^2}{2m} + \frac{m\omega^2\hat{x}^2}{2},
\]
is written as
\[
\hat{H} = \hbar\omega \left( \hat{N} + \frac{1}{2} \right) \tag{5}
\]
where \( \hat{N} = \hat{a}^\dagger \hat{a} \) is the number operator.
5. **Hermitian Nature of \( \hat{N} \)**:
-
Expert Solution
arrow_forward
Step 1
The operators can be expressed as,
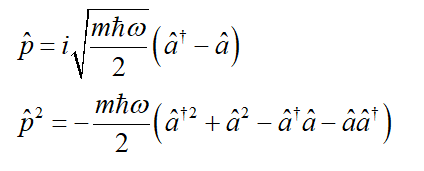
Trending nowThis is a popular solution!
Step by stepSolved in 3 steps with 3 images

Knowledge Booster
Similar questions
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios