1.The odd parity eigenstates of the infinte square well , with potential V = 0 in the range −L/2 ≤ ? ≤ L/2, are given by :
(see figure)
and have Ψn(x, t) = 0 elsewhere , for n=2 , 4 , 6 etc
a) Sketch the potential of this system , including in your sketch the positions of the lowest three energy levels . Indicate in your sketch the form of the wavefunction for a particle in each of these energy levels , and state which of the wavefunctions you have drawn could be decirbed by the Ψn written above (see figure) .
b) Calculate the expectation value of momentum , ⟨p⟩ for a particle with n=2
c) Calculate the expectation value of momentum squared ⟨p 2⟩ , for a particle with n = 2 .
Hint : you may use the mathematical identiy sin2 x = 1/2 (1 − cos 2x) without proof .
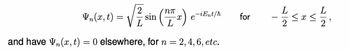
Step by stepSolved in 2 steps with 2 images

- Consider a particle in a one-dimensional rigid box of length a. Recall that a rigid box has U (x) = 00 for x a, and U () = 0 for 0 )arrow_forward7. Consider a particle in an infinite square well centered at x = 0 in one of its stationary states. For this problem, you may look up any integrals. Some useful ones are given in Harris. a) Compute (x) and (pr) for arbitrary n. Do this by direct computation but then describe how you could have found these results using symmetry (the symmetry can either be symmetry in the physical system, such as the shape of the wave function, or symmetry related to the expectation value integral, such as the shape of the integrand). b) Using your answer to part a), show that the uncertainty in the momentum is Apx nh for arbitrary n. Do this two ways: (i) first by using your answer to part a) and directly computating (p2) (via an integral) and (ii) by using your answer to part a) and relating (p2) to the kinetic energy operator. c) Show that the uncertainty principle holds for the ground state. 2L -arrow_forwardAn electron is confined to a 1-dimensional infinite potential well of dimensions 1.55 nm. Find the energy of the ground state of the electron. Give your answer in units of electron volts (eV). Round your answer to 2 decimal places. Add your answerarrow_forward