**Problem Statement:**1. Refer to figures 1 and 2. Calculate the magnitude of force needed to displace the block by 12.0 cm. What is the maximum kinetic energy this object can attain? What is its maximum potential energy? What is the amplitude? Where would you find the maximum and minimum potential and kinetic energies? If the angular frequency is 10.0 rad/sec, calculate the mass of the object.---**Figure 1:**The image shows a block attached to a spring on a flat surface. The spring is coiled and attached to one end, with the block on the other, indicating a classic spring-mass system.---**Hooke's Constant Plot:**- **Graph Explanation:** - The graph is labeled "Hooke's Constant Plot." - The y-axis represents the Force (N), ranging from 0.00 to 6.00 N. - The x-axis represents the Displacement (cm), ranging from 0.00 to 5.00 cm. - The plot is a straight line indicating a linear relationship between force and displacement, consistent with Hooke's Law (F = kx).This graph can be used to determine the spring constant (k) by calculating the slope of the line (change in Force divided by change in Displacement).---To solve the problem:- **Force Calculation:** - Use Hooke's Law: F = kx. - Determine the spring constant (k) from the slope of the graph.- **Maximum Kinetic and Potential Energy:** - Maximum Potential Energy at maximum displacement: PE_max = (1/2)kx^2. - Maximum Kinetic Energy when all potential energy is converted: KE_max = PE_max.- **Angular Frequency and Mass:** - Use the formula for angular frequency in terms of mass and spring constant: ω = sqrt(k/m). - Rearrange to solve for mass (m): m = k/ω^2.These steps will guide the calculation of the required physical quantities.

Name: **Problem Statement:**1. Refer to figures 1 and 2. Calculate the magn
Uploaded: 2024-03-20T06:58:04.000Z
Channel: Bartleby
Description: **Problem Statement:**1. Refer to figures 1 and 2. Calculate the magnitude of force needed to displace the block by 12.0 cm. What is the maximum kinetic energy this object can attain? What is its maximum potential energy? What is the amplitude? Wher

The given graph is :The formula for the potential energy is also

Science

Physics

1. Refer and use figure 1 and 2. Calculate the magnitude of force needed to displace the block by 12.0 cm. What is the maximum kinetic energy this object can attain? What is its maximum potential energy? What is the amplitude? Where you would find the maximum and minimum potential and kinetic energies? If the angular frequency is 10.0 rad-sec¹, calculate the mass of the object. Figure 1: Hooke's Constant Plot

1. Refer and use figure 1 and 2. Calculate the magnitude of force needed to displace the block by 12.0 cm. What is the maximum kinetic energy this object can attain? What is its maximum potential energy? What is the amplitude? Where you would find the maximum and minimum potential and kinetic energies? If the angular frequency is 10.0 rad-sec¹, calculate the mass of the object. Figure 1: Hooke's Constant Plot

College Physics

11th Edition

ISBN:9781305952300

Author:Raymond A. Serway, Chris Vuille

Publisher:Raymond A. Serway, Chris Vuille

Chapter1: Units, Trigonometry. And Vectors

Section: Chapter Questions

Problem 1CQ: Estimate the order of magnitude of the length, in meters, of each of the following; (a) a mouse, (b)...

See similar textbooks

Related questions

Q: Hooke's Law defines the force applied by an ideal spring: FH = -KAX, where FH is the force applied…

Q: The figure below shows a ball with mass m = 0.402 kg attached to the end of a thin rod with length L…

A: mass of ball (m) = 0.402 kg L = 0.506 m

Q: Q8: A piston executes simple harmonic motion with an amplitude of 0.5 m. If it passes the center of…

Q: ry AX Bookmarks Profiles Tab Window ★ --- Assignments Item 9…

Q: Chapter 15, Problem 058 For a damped oscillator with a mass of 240 g, a spring constant 130 N/m and…

A: Solution: Given Values, Mass(m)=240 g=0.24 Kg Spring constant(k)=130 N/m Damping…

Q: Force vs. Elongation A B Elongation (m) 7. What physical quantity is represented by the slope of…

Q: A damped oscillation is driven by an extemal force F) - re given in Sl units. Which of the following…

A: FD(t) = F cos(ωd *t + φ') , where φ' is the phase difference hence from this equation, it is…

Q: Given: ASF. Rod mass = 10 kg. A couple, M is applied. The rod started from rest with spring…

Q: If bar AB has an angular velocity wAB = 6 rad/s, determine the velocity of the slider block Cat the…

A: Here we will use sine law. And some basic formula

Q: Tactics Box 5.3 Working with Ropes and Pulleys 5 of 23 • The strings are massless, and • The pulleys…

Q: At which position does the bob have its maximum kinetic energy? A) 1 B) 2 C) 3 D) 4

A: As per guidelines in case of multiple questions, first one is mandatory to solve. Given Pendulum…

Q: object with one end of a light horizontal spring attached to it rests on a frictionless surface. The…

A: According to Hook's law F = kx Energy stored in spring U = (1/2)kx2

Q: 4. An object of mass m is pressed against a spring compressing the spring a distance d and giving it…

A: 4) The potential energy of a spring is given by, U = ½ × k × x2 where, k is spring constant, x is…

Q: For spring in series: a. Draw the figure of spring in series. b. Derive the equivalent spring…

A: following is the figure for springs connected in series

Q: kum The mass of the block depicted in the image is 1.08 kg. The spring has a spring constant of 78.1…

Q: A student is doing a physics experiment with a pendulum in the car ride home from school. At one…

A: Givenm=1.4 kgθ=24∘

Q: 4. A wheel, with radius R= 0.5 m, initially has an angular velocity of 2.5 rev/s, and is slowing…

Q: Mass vs. Periðd 4. .****** ..**... ........ What would the units of slope be for this graph? 6 8…

A: The tangent is the slop of each and every graph. The tangent is the ratio of perpendicular to the…

Q: Q5: Determine the speed of slider at position 2 when slider weight 0.75 kg and P=300 N. The slider…

A: SOlution: given that P = 300 N W = 0.75 kg k = 210 N/m L =200 m

Q: 1. An engineer working at an industrial spring company designs a spring that obeys a force law F (x)…

A: In this question we are given that an engineer is working at an industrial spring company designs a…

Q: package is being vibrated on a vibration table. Accelerometers are attached to the table and the…

A: An accelerometer is an instrument that evaluates a structure's vibration or acceleration of motion.…

Q: Determine the specifications (unstretched length and spring constant k) for the elastic cord to be…

A: total height of platform=45 m max. allowable mass= 100 Kg height of man= 0 m k=200 N/m

Q: What is the maximum acceleration of a platform that oscillates at amplitude 2.20 cm and frequency…

A: The oscillating platform has an amplitude of 2.2 cm A=2.2 cm=2.2×10-2 m This platform is oscillating…

Q: 25. A 1.0 kg block is attached to an unstretched spring of spring constant 50 N/m and released from…

A: The change in the height of the block can be expressed as below,

Q: YOU MUST ONLY USE ENERGY CONCEPTS TO COMPLETE THE PROBLEMS BELOW. 3. A 55 kg man is standing on a…

Q: Op

A: It is a practicle question required stopwatch, spring , mass. for different amplitude measure the…

Q: The figure below shows two identical blocks with mass m connected to a spring with spring constant…

A: Given information: The mass of the spring = m The spring constant = k The acceleration due to…

Q: You have landed on an alien planet and because you have nothing better to do with your time, yoù…

A: Given,The mass of the block, m = 1701 kgThe coefficient of friction, μs=0.9The spring constant, k =…

Q: Needs Complete solution with 100 % accuracy.

A: A block is attached to a spring . Which is sliding back and forth on a frictionless surface.The…

Q: Problem 1: A mass m is attached to a spring with spring constant k. The mass oscillates without…

Q: Q3: State whether the following statement is True or False 1 If P₁ + P₂ = constant, then the net…

Q: A 3 kg object connected to a light spring with a spring constant of 120 N/m oscillates on a…

Q: answer this show full steps

A: SolutionThe package compresses the spring at a distance of approximately 0.49 meters (based on the…

Q: Q1. Hooke's Law a) Calculate the magnitude of the force required to stretch a 20cm long spring with…

Q: Calculate the following questions below. Encircle or highlight the answer and round off in two…

Q: Examine the situation below. Using the information provided, determine... a. The speed at point A.…

A: We need to apply the law of conservation of energy to solve the given problem.

Q: Which of the following explanations describes the potential and kinetic energy at each position? A.…

A: For a pendulum the kinetic energy will be highest at the mean position and zero at the extreme…

Q: Assuming this maximum height was the result of one push from her parent, what was the average force…

A: Given data, distance S=152 cm

Q: The piston in the cylinder head of locomotive has a stroke (twice the amplitude) of 0.65 m. If the…

Q: 3. A mass 2.5 kg is suspended through a vertical spring experiences simple harmonic motion with…

A: Please see the solution below.

Q: Which of the graphs below describes the energy of the pendulum at the highest point of its arc? A B…

A: Given data: The pendulum is at highest point of its arc Required: The kinetic energy and potential…

Concept explainers

Simple harmonic motion

Simple harmonic motion is a type of periodic motion in which an object undergoes oscillatory motion. The restoring force exerted by the object exhibiting SHM is proportional to the displacement from the equilibrium position. The force is directed towards the mean position. We see many examples of SHM around us, common ones are the motion of a pendulum, spring and vibration of strings in musical instruments, and so on.

Simple Pendulum

A simple pendulum comprises a heavy mass (called bob) attached to one end of the weightless and flexible string.

Oscillation

In Physics, oscillation means a repetitive motion that happens in a variation with respect to time. There is usually a central value, where the object would be at rest. Additionally, there are two or more positions between which the repetitive motion takes place. In mathematics, oscillations can also be described as vibrations. The most common examples of oscillation that is seen in daily lives include the alternating current (AC) or the motion of a moving pendulum.

Topic Video

Question

**Problem Statement:**

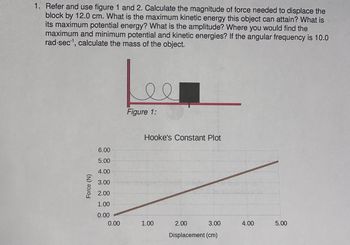
1. Refer to figures 1 and 2. Calculate the magnitude of force needed to displace the block by 12.0 cm. What is the maximum kinetic energy this object can attain? What is its maximum potential energy? What is the amplitude? Where would you find the maximum and minimum potential and kinetic energies? If the angular frequency is 10.0 rad/sec, calculate the mass of the object.

---

**Figure 1:**

The image shows a block attached to a spring on a flat surface. The spring is coiled and attached to one end, with the block on the other, indicating a classic spring-mass system.

---

**Hooke's Constant Plot:**

- **Graph Explanation:**
- The graph is labeled "Hooke's Constant Plot."
- The y-axis represents the Force (N), ranging from 0.00 to 6.00 N.
- The x-axis represents the Displacement (cm), ranging from 0.00 to 5.00 cm.
- The plot is a straight line indicating a linear relationship between force and displacement, consistent with Hooke's Law (F = kx).

This graph can be used to determine the spring constant (k) by calculating the slope of the line (change in Force divided by change in Displacement).

---

To solve the problem:

- **Force Calculation:**
- Use Hooke's Law: F = kx.
- Determine the spring constant (k) from the slope of the graph.

- **Maximum Kinetic and Potential Energy:**
- Maximum Potential Energy at maximum displacement: PE_max = (1/2)kx^2.
- Maximum Kinetic Energy when all potential energy is converted: KE_max = PE_max.

- **Angular Frequency and Mass:**
- Use the formula for angular frequency in terms of mass and spring constant: ω = sqrt(k/m).
- Rearrange to solve for mass (m): m = k/ω^2.

These steps will guide the calculation of the required physical quantities.

Expert Solution

This question has been solved!

Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.

This is a popular solution!

SEE SOLUTION Check out a sample Q&A here

Step 1: Determine the given variable

VIEW

Step 2: Calculate the force needed to displace the block by 12 cm

VIEW

Step 3: Calculate the maximum kinetic energy that the object can attain :

VIEW

Step 4: Calculate the maximum potential energy that the object can attain :

VIEW

Step 5: Determine where you can find maximum and minimum of kinetic energy and potential energy

VIEW

Step 6: Find mass of object

VIEW

Solution

VIEW

Trending now

This is a popular solution!

Step by step

Solved in 7 steps with 8 images

SEE SOLUTION Check out a sample Q&A here

Knowledge Booster

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.

Similar questions

Automatic Zoom 9. Students are given a pendulum. The teacher also provides students with a pictorial model labeled A, 0, and B. Each letter signifies the position of the pendulum. Part A. Which of the following explanations describes the potential and kinetic energy at each position? A. The potential energy is greatest at O and the kinetic energy is equal at A and B. B. The potential energy is greatest at A, followed by B, and then O. C. The kinetic energy is greatest at O, followed by B. and then A D. The potential energy is equal at A and B and the kinetic energy is greatest at O. Part B. What factors could students adjust to explain the transformation between potential and kinetic energy? A. Students could push the pendulum instead of releasing it from position A to increase the kinetic energy at position O. B. Students could move position A higher which would increase the kinetic energy at position O. C. Students could increase the length of the string which would increase the…
At full swing, a pendulum 8m long, subtends an angle of 34 degrees. How high does the bob of the pendulum rise above its rest position? Use below correct choices as answer and show solution; a.) 55 m b) 45 m c) 35 m d) 25 m
An object with a mass of 2400 g is attached to a spring with a spring constant of 360 N/m. When the object is 15 cm from its equilibrium position, it is moving with a speed of 500 cm/sec. Show all work for full credit. a. What is the amplitude? (in cm) b. What the maximum velocity the object travels? (in cm/sec)
Below is the depicted graph of the velocity of a block that is connected to a spring with an unspecified mass and a force constant of 80 N/m, undergoing oscillation. The time axis is wrongly marked for 1.6 sec. It should be 1.8 sec. Determine the period, frequency, and angular frequency of oscillation? Calculate the maximum displacement of the mass from equilibrium in centimeters? Just so you know: It does not correspond to the amplitude of the velocity graph. What is the peak acceleration of the mass and identify the moments when it transpires?
I just need the answer for question #30 please Thank you
ACTIVITY 3 Problem Solving Gravitational Potential Energy and Elastic Potential Energy Energy is the ability to produce changes in matter. It has two states, the kinetic energy and potential energy. Kinetics energy has 3 forms, vibrational, rotational, and translational, While potential energy has 3 types, gravitational, chemical, and elastic potential energy. Gravitational PE is the energy stored because of its height and elastic PE is the energy stored in elastic materials as the result of their stretching or compressing. nga Read, analyze, and solve the following problems using the GUFSA template. Show your complete solution. Round off your final answer to the nearest hundredths. A. GPE woH 1. How much G.P.E. does a 100 kg boulder that is 75m above the ground has?
Two identical springs are connected in parallel as shown, each spring has a spring constant of 30 N/m. What is the spring constant of the overall two-spring system, in N/m? needed. Do not include the positive sign if the answer is positive. No unit is Your answer needs to have 2 significant figures, including the negative sign in your answer needed in your answer, it is already given in the question statement.
Estimate the stiffness of the spring, kk (in N/m) in a child’s pogo stick if the child has a mass of 27 kg and bounces once every 2.6 seconds. Type your answer to within one decimal place. Use a period (full stop) for a decimal place, eg. 500.0 - Do not use a comma or input your answer in some form of scientific notation. Do NOT include units in your answer.
A 20kg block starts from rest and slides 6m down an incline as shown below. The block then hits a spring that has a force constant of 200 N/m. The angle of the incline is 30° and there is a coefficient of kinetic friction equal to 0.2 between the block and the incline. HK = 0.2 6m K = 200N/m www 300 Answer the following questions on your own paper and staple it to this sheet. 1. What is the speed of the block as it hits the spring? 2. At what distance from the top does the maximum speed occur? 3. What is the maximum speed of the block? 4. What is the total distance that the spring gets compressed? The spring recoils to push the block back up the incline. 5. What will be the speed of the block when it leaves the spring? 6. How far up the incline will the block travel? (above the spring)
Mass and Spring System and Pendulum 4. Find the period and frequency of a simple pendulum 1.000 m long at a location where g = 9.8 m/s². Show your solution and answer:
A block of mass m is placed on a smooth inclined plane, which is at an angle, with respect to the horizontal, as shown in Figure 2. A spring with force constant k is attached to the bottom of the incline. spring. block Hellll Ꮎ Figure 2 Sketch of the block, inclined plane and spring, for use in Question 9.
Computer Lab: Undamped Spring Use Part 1.7 of IDE Lab 9 to visualize how the potential and kinetic energies of a mass-spring system change during an oscillation but maintain a constant total energy. • L i n e a r O s c i l l a t i o n s : F r e e R e s p o n s e Lab 9 clarifies the energies.