
Algebra and Trigonometry (6th Edition)
6th Edition
ISBN: 9780134463216
Author: Robert F. Blitzer
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Question
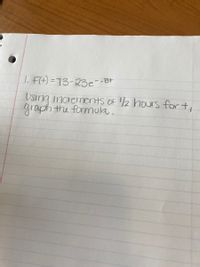
Transcribed Image Text:The image contains handwritten text that outlines a mathematical task. The task is as follows:
1. \( F(t) = 73 - 23e^{-0.8t} \)
Instructions: Using increments of 1/2 hours for \( t \), graph the formula.
Explanation for Educational Website:
This is a mathematical exercise involving an exponential function. The equation \( F(t) = 73 - 23e^{-0.8t} \) represents a function where \( F(t) \) is dependent on the variable \( t \), typically representing time.
The goal is to graph this function, plotting the values of \( F(t) \) at increments of 0.5 hours, using the specified formula.
To graph it:
1. Calculate the value of \( F(t) \) for \( t = 0, 0.5, 1.0, 1.5, \ldots \).
2. Plot these points on a graph with \( t \) on the x-axis and \( F(t) \) on the y-axis.
3. Connect these points to visualize the behavior of the function over time.
4. Observe the trend and shape of the graph, noting the effect of the exponential term \( e^{-0.8t} \) on the function’s rate of change.
This exercise helps in understanding how to evaluate and graph exponential functions incrementally.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 3 steps with 3 images

Knowledge Booster
Similar questions
- The deck of a bridge is suspended 285 feet above a river. If a pebble falls off the side of the bridge, the height, in feet, of the pebble above the water surface after t seconds is given by y = 285 − 16t2. (a) Find the average velocity (in ft/s) of the pebble for the time period beginning when t = 2 and lasting the following amount of time. (i) 0.1 seconds (ii)0.05 seconds (iii)0.01 seconds (b) Estimate the instantaneous velocity (in ft/s) of the pebble after 2 seconds.arrow_forwardDuring Ricardo noticed an ink stain with a diameter of about 3 cm on the front of his teacher’s shirt. He then noticed that there was a pen in the pocket and that the ink blot was continuing to spread across the front of the teacher’s shirt. He estimated that the diameter of the ink blot seemed to be growing by about 0.5 cm every 2 minutes. a) Write an equation for the RADIUS, r, of the ink stain, as a function of time, t. Assume that t = 0 represents the time that Ricardo first noticed the ink stain. b) Write an equation showing the AREA, A, of the ink stain as a function of the time t. (Hint: It might help to first write A as a function of r. ) c) Draw a graph of the function A(t) for 10 minutes. d) At what time is the area of the ink stain about 25 square centimeter? Show how you answer this question. (i.e. ”I found it using desmos” is not sufficient)arrow_forwardPlease graph the function of D(t)= 28sin(360/365 t - 1.4)arrow_forward
- I need to graph Y=-4/x I'm not understanding how to decide what imputs to use for x. Where does this imput come from and how to determine what to use?arrow_forwardSketch a graph of the function g(x)=-2sin(1/4x - pi/4)+1. Be sure to label the scale on the axes and draw at least two cycles.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON
Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning
Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON
Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press
Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education
College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education

Algebra and Trigonometry (6th Edition)
Algebra
ISBN:9780134463216
Author:Robert F. Blitzer
Publisher:PEARSON

Contemporary Abstract Algebra
Algebra
ISBN:9781305657960
Author:Joseph Gallian
Publisher:Cengage Learning

Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning

Algebra And Trigonometry (11th Edition)
Algebra
ISBN:9780135163078
Author:Michael Sullivan
Publisher:PEARSON

Introduction to Linear Algebra, Fifth Edition
Algebra
ISBN:9780980232776
Author:Gilbert Strang
Publisher:Wellesley-Cambridge Press

College Algebra (Collegiate Math)
Algebra
ISBN:9780077836344
Author:Julie Miller, Donna Gerken
Publisher:McGraw-Hill Education