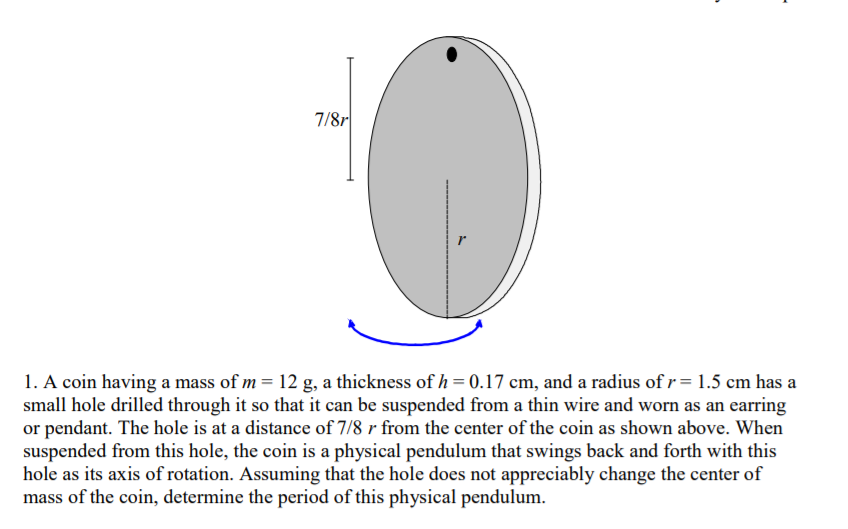
1. A coin having a mass of m = 12 g, a thickness of h = 0.17 cm, and a radius of r= 1.5 cm has a small hole drilled through it so that it can be suspended from a thin wire and worn as an earring or pendant. The hole is at a distance of 7/8 r from the center of the coin as shown above. When suspended from this hole, the coin is a physical pendulum that swings back and forth with this hole as its axis of rotation. Assuming that the hole does not appreciably change the center of mass of the coin, determine the period of this physical pendulum.

A physical pendulum is constructed such that two spheres of different radii are welded together.  A rod is then welded to the top of these two spheres as shown.  The length of the rod is 2.90 m while the mass is 2.00 kg.  The radius of the small (upper) sphere is 0.790 m with a mass of 8.20 kg.  The radius of the lower (larger) sphere is 0.960 m with a mass of 11.6 kg.  The entire system is hung from the end of the rod.   a. what is the rotational intertia of the rod?   b. what is the rotational intertial of the small sphere?   c. what is the rotational intertia of the large sphere?   d. what is the distance from the pivot point to the center of mass of the system?   e. what is the period of oscillation of the pendulum?

In the figure, a solid cylinder attached to a horizontal spring (k = 5.80 N/m) rolls without slipping along a horizontal surface. If the system is released from rest when the spring is stretched by 0.290 m, find (a) the translational kinetic energy and (b) the rotational kinetic energy of the cylinder as it passes through the equilibrium position. (c) If the cylinder has mass M = 6.20 kg, find the period of the simple harmonic motion that the cylinder's center of mass executes. (Hint: Find the time derivative of the total mechanical energy.) M · k oooooo (a) Number i 0. (b) Number i (c) Number i O. Units Units Units

In the figure, a solid cylinder attached to a horizontal spring (k = 9.00 N/m) rolls without slipping along a horizontal surface. If the system is released from rest when the spring is stretched by 0.250 m, find (a) the translational kinetic energy and (b) the rotational kinetic energy of the cylinder as it passes through the equilibrium position. (c) If the cylinder has mass M = 5.30 kg, find the period of the simple harmonic motion that the cylinder's center of mass executes. (Hint: Find the time derivative of the total mechanical energy.) (a) Number i Units (b) Number i Units (c) Number i Units >