Question
A wagon wheel is constructed
as shown in Fig.. The radius of
the wheel is 0.300 m, and the rim has
mass 1.40 kg. Each of the eight spokes
that lie along a diameter and are 0.300 m
long has mass 0.280 kg. What is the
moment of inertia of the wheel about
an axis through its center and perpendicular
to the plane of the wheel?
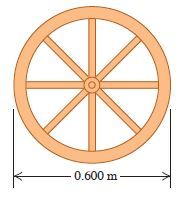
Transcribed Image Text:0.600 m-
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 4 steps with 5 images

Knowledge Booster
Similar questions
- An approximate model for a ceiling fan consists of a cylindrical disk with four thin rods extending from the disk's center, as in the figure below. The disk has mass 2.30 kg and radius 0.200 m. Each rod has mass 0.850 kg and is 0.840 m long. HINT (a) Find the ceiling fan's moment of inertia about a vertical axis through the disk's center. (Enter your answer in kg. m².) kg - m² (b) Friction exerts a constant torque of magnitude 0.113 Nm on the fan as it rotates. Find the magnitude of the constant torque provided by the fan's motor if the fan starts from rest and takes 15.0 s and 16.5 full revolutions to reach its maximum speed. (Enter your answer in N. m.) N.marrow_forwardThree objects are spinning as shown in the figure. Each object has a total mass of m and a radius of R. The object on the left is a hoop with its mass evenly distributed around the rim. The object in the middle is a solid sphere with its mass evenly distributed throughout. The object on the right consists of a massless rod 2R long with a point mass of 0.5m attached to each end. Which object has the greatest moment of inertia and which one the least? Mass m Mass = m Mass = 0.5m The rod + masses is the largest; the hoop is the smallest The sphere is the largest, the hoop is the smallest The hoop is the largest; the rod + masses is the smallest The hoop is the largest; the sphere is the smallest The rod + masses is the largest; the sphere is the smallestarrow_forwardConsider the setup shown below. The blocks have masses 3.6 kg and 24 kg. The pulley has mass 7.4 kg, and is a uniform disc with radius 0.23 m. Assume the pulley to be frictionless, but the coefficient of friction between the block and the surface is 0.36. What is the acceleration of the blocks? Assume the 24 kg mass is descending with acceleration a. The moment of inertia of the disk is 1/2MR2 and the acceleration of gravity is 9.8 m/s2.arrow_forward
- Two Thin rectangular sheets (0.28m x 0.47 m) are identical. In the first sheet the axis of rotation lies along the 0.28 inside, and in the second it lies along 0.47m side. The same torque is applied to each sheet. The first sheet starting from rest reaches its final angular velocity in 5.2 s. How long does it take for the second seat starting from rest to reach the same Angularer velocity?arrow_forwardProblem 2. Three forces are applied to a disk of radius 0.35 m and mass 2.5 kg, as shown in figure below. One force is perpendicular to the rim, one is tangent to it, and the other one makes a 40.0° angle with the radius. The moment of inertia of a disk about its center is I = (1/2)MR². (a) What is the net torque on the disk due to these three forces for an axis perpendicular to the disk and passing through its center? (b) What is the angular acceleration of the disk? 11.9 N 0.350 m 40.0° 14.6 N 8.50 Narrow_forwardThe figure below shows a side view of a car tire before it is mounted on a wheel. Model it as having two sidewalls of uniform thickness 0.600 cm and a tread wall of uniform thickness 2.50 cm and width 19.8 cm. Assume the rubber has a uniform density 1.10 x 10³ kg/m³. Find its moment of inertia about an axis perpendicular to the page through its center. 0.082 x Your response differs significantly from the correct answer. Rework your solution from the beginning and check each step carefully. kg - m² 33.0 cm 30.5 cm 16.5 cm Sidewall Treadarrow_forward
- A solid cylinder with mass m, radius R, and rotational inertia I (about its center) is released from rest and rolls down a ramp. Friction between the bottom of the cylinder and the ramp causes the cylinder to roll without slipping. The linear acceleration of the cylinder is a. Which TWO of the equations below are correct for this scenario? The equations are in terms of m, I, R, and a, as well as f (the force of static friction between the cylinder and the ramp) and g. (You must pick BOTH of them to get this question correct!) f = ma mg sin θ = ma mg sin θ - f = ma f R = I (a/R) mg sin θ - f = I (a/R) R mg sin θ = IaRarrow_forwardA helicopter has two blades (see figure), each of which has a mass of 270 kg and can be approximated as a thin rod of length 6.7 m. The blades are rotating at an angular speed of 51 rad/s. (a) What is the total moment of inertia of the two blades about the axis of rotation? (a) Determine the rotational kinetic energy of the spinning blades. 2arrow_forwardA wheel consists of a rim (ring) with a mass of 1.3kg and a radius of 0.45m and four equally-spaced spokes (rods) that run from the center of the wheel to the edge of the rim. Each spoke has a mass of 0.15kg and a length equal to the radius of the wheel. What is the total rotational inertia of the wheel about its center?arrow_forward
arrow_back_ios
arrow_forward_ios