A pond is approximately circular, with a diameter of 400 feet. Starting at the center, the depth of the water is measured every 25 feet and recorded in the table (a) Use the regression capabilities of a graphing utility to find a quadratic model for the depths recorded in the table. Use the graphing utility to plot the depths and graph the model. (b) Use the integration capabilities of a graphing utility and the model in part (a) to approximate the volume of water in the pond. (c) Use the result of part (b) to approximate the number of gallons of water in the pond.
With differentiation, one of the major concepts of calculus. Integration involves the calculation of an integral, which is useful to find many quantities such as areas, volumes, and displacement.
Expert Solution
Step 1
The given data,
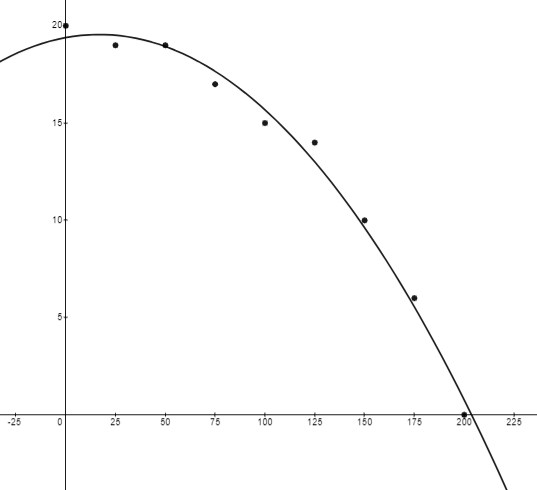
x
0
25
50
75
100
125
150
175
200
Depth
20
19
19
17
15
14
10
6
0
We have to find,
(a) The regression equation for a quadratic model for the depths recorded in the table.
(b) Using the integration capabilities of a graphing utility and the model in part (a) we have to approximate the volume of water in the pond.
(c) Use the result of part (b) to approximate the number of gallons of water in the pond.
Step 2
a)
The given data,
x
0
25
50
75
100
125
150
175
200
Depth
20
19
19
17
15
14
10
6
0
Using the regression calculator,
The quadratic model for the depths is recorded in the table is .
Graph of the depths and the quadratic model.
Step 3
b)
The formula for the volume of water in the pond is,
.
Here and .
Now,
Solve this integral we get
The volume of water in the pond is .
Step by step
Solved in 5 steps with 1 images
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.
