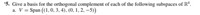
. Give a basis for the orthogonal complement of each of the following subspaces of Rª. a. V = Span ((1, 0, 3, 4), (0, 1, 2, -5))

1. Let W be the subspace of R1 spanned by wi = (1, –1,0,5) and w2 = (2, 1, 3, 4). Find a basis for its orthogonal complement Wl.

(1, 1,0,0,0) be two binary vectors. Compute the Hamming 3. Let y = (1,0,0,0, 1) and z = distance and the Jaccard distance between y and z manually. (Do not use R.)

4. Let S = {v,,v2, V3, V4, V5} where, 3 1 2 3 3 ,V2 9. ,V3 2 la -1 4 Find a basis for the space span(S) which is a subset of S. Then express each vector that is not in the basis as a linear combination of the basis vectors.

1. Determine whether the vectors (1,-1) and (1, 1)T are linearly inde- pendent or not. 2. Show that the vectors (1,0,0), (1, 1, 0) and (1,1,1) form a basis of R³. 3. Suppose that the vectors (1, 2, -1,0) and (1,3,2,0) span the sub- space U of R4. Determine whether the vector (1, 1, 1, 0) belongs to U or not.

Determine whether the following set of vectors in IR³: a. spans R³ b. Is linearly independent. c. Is a basis for R³ S = {(1,2,3), (0,1,0), (-1,0, -1)}

1. Consider the vector space R³. Find all values of c such that the vector (2c², -3c, 1) = span({(1, 1, 3), (0, 1, 1), (1, 2, 4)}).

1) Show that the following three vectors are coplanar. u=(2, 3,-1) v= (0, 1, -2) w=(2, 4, -3).

Find a basis for the subspace of R° spanned by the following vectors. 7 2 18 -3 -3 6 -18 -18 12 -14 14 { Basis: