
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
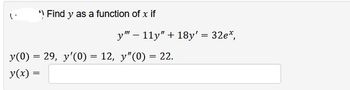
Transcribed Image Text:*) Find y as a function of x if
y" 11y" + 18y' = 32e*,
y(0) = 29, y'(0) = 12, y"(0) = 22.
y(x) =
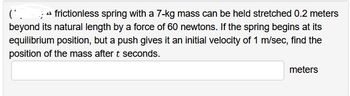
Transcribed Image Text:(*. frictionless spring with a 7-kg mass can be held stretched 0.2 meters
beyond its natural length by a force of 60 newtons. If the spring begins at its
equilibrium position, but a push gives it an initial velocity of 1 m/sec, find the
position of the mass after t seconds.
meters
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps with 2 images

Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
in b part, system gives an error that t is not defined for the frictionless spring question.
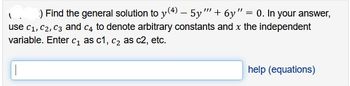
Transcribed Image Text:-
) Find the general solution to y(4) — 5y"' + 6y" = 0. In your answer,
use C₁, C2, C3 and c4 to denote arbitrary constants and x the independent
variable. Enter c₁ as c1, c₂ as c2, etc.
help (equations)
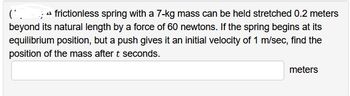
Transcribed Image Text:(*. frictionless spring with a 7-kg mass can be held stretched 0.2 meters
beyond its natural length by a force of 60 newtons. If the spring begins at its
equilibrium position, but a push gives it an initial velocity of 1 m/sec, find the
position of the mass after t seconds.
meters
Solution
by Bartleby Expert
Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
in b part, system gives an error that t is not defined for the frictionless spring question.

Transcribed Image Text:-
) Find the general solution to y(4) — 5y"' + 6y" = 0. In your answer,
use C₁, C2, C3 and c4 to denote arbitrary constants and x the independent
variable. Enter c₁ as c1, c₂ as c2, etc.
help (equations)

Transcribed Image Text:(*. frictionless spring with a 7-kg mass can be held stretched 0.2 meters
beyond its natural length by a force of 60 newtons. If the spring begins at its
equilibrium position, but a push gives it an initial velocity of 1 m/sec, find the
position of the mass after t seconds.
meters
Solution
by Bartleby Expert
Knowledge Booster
Similar questions
- A large cruise ship of mass 6.70 ✕ 107 kg has a speed of 10.8 m/s at some instant. (a) What is the ship's kinetic energy at this time? J(b) How much work is required to stop it? (Give the work done on the ship. Include the sign of the value in your answer.) J(c) What is the magnitude of the constant force required to stop it as it undergoes a displacement of 2.00 km? Narrow_forwardA mass of 3 kg is suspended from a spring whose constant is 2 Nt/cm. The system is then immersed in a medium that imparts a damping force equal to 1.2 times the instantaneous velocity. The mass is released from 5 cm above the equilibrium positon with downward velocity 50 cm/sec. Determine the position of the mass at any time t.arrow_forward2. If an iron ball of weight W = 89 kg-m/sec2 (=Mg [mass x gravitational constant]) stretches a spring 10.00 cm, how many cycles per minute will this mass-spring system execute? What will its motion be if we pull down the weight an additional 15.0 cm ? (30 points)arrow_forward
- A force of 13 pounds stretches a spring 1 foot. A mass weighing 6.4 pounds is attached to the spring, and the system is then immersed in a medium that offers a damping force numerically equal to 1.6 times the instantaneous velocity. (a) Find the equation of motion if the mass is initially released from rest from a point 1 foot above the equilibrium position. (b) Express the equation of motion in the form (c) Find the first time at which the mass passes through the equilibrium position heading upward. (Round your answer to three decimal places.)arrow_forwardA mass weighing 16 pounds stretches a spring feet. The mass is initially released from rest from a point 4 feet below the equilibrium position, and the subsequent motion takes place in a medium that offers a 1 damping force that is numerically equal to - the instantaneous velocity. Find the equation of motion x(t) if the mass is driven by an external force equal to f(t) = 20 cos(3t). (Use g = 32 ft/s? for the acceleration due to gravity.) x(t) = ftarrow_forwardA mass weighing 8 pounds is attached to a spring whose constant is 4 lb/ft. The medium offers adamping force that is numerically equal to the two times instantaneous velocity. The mass is initiallyreleased from a point 1 foot above the equilibrium position with a downward velocity of 8 ft/s.(a) Specify the 2nd order DE as an IVP for the mass spring system.(b) Solve the equation to find the position of the mass at any time t.(c) Determine the time at which the mass passes through the equilibrium position.(d) Find the time at which the mass attains its extreme displacement from the equilibrium position. Whatis the position of the mass at this instant?arrow_forward
- A mass weighing 16 pounds stretches a spring 8 feet. The mass is initially released from rest from a point 4 feet below the equilibrium position, and the subsequent motion takes place in a medium that offers a 1 damping force that is numerically equal to - the instantaneous velocity. Find the equation of motion x(t) if the mass is driven by an external force equal to f(t) = 20 cos(3t). (Use g = 32 ft/s2 for the acceleration 2 due to gravity.) x(t) = ftarrow_forwardA mass weighing 24 pounds, attached to the end of a spring, stretches it 4 inches. Initially, the mass is released from rest from a point 8 inches above the equilibrium position. Give the initial conditions. (Use g = 32 ft/s2 for the acceleration due to gravity.)arrow_forwardImagine a diver jumping off a spring board that is 10 feet above the water. The board throws the diver up with an upward velocity of 9 feet per second. That means that if there were no gravity, the diver would keep going up at the rate of 9 feet every second. Fortunately for the diver, there is gravity. Eventually, gravity over comes the force of the diving board and the the diver begins to come down. So over all, the diver is thrown into the air fairly quickly, he slows down until he stops, then begins to come back down (slowly at first, then faster and faster until he hits the water). The height of any object like the diver that is projected into the air can be modeled with the following function: h(t) = -16t^2 + v*t + m In this function: h(t) is the height of the object t seconds after it was thrown into the air. t is the number of seconds after the object was thrown in the air. v is the initial upward velocity (for the diver this was 9 ft per second). m is the initial height of the…arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

