
The tip of a one-link robot is located at
FIGURE P6.1 Rotating one-link robot starting at
To plot:
The
Answer to Problem 1P
The graph for
The graph for
The amplitude of sine and cosine function is
Explanation of Solution
Given:
The tip of a one-link robot is initially located at

Time taken for the robot to move form
A one-link robot is length of
Concept used:
Write the expression for the linear frequency.
Here,
Write the expression for the angular frequency.
Here,
Write the expression for the time period.
Write the expression for
Here,
Write the expression for
Here,
Write the expression for the time shift.
Here,
Calculation:
The one-link robot completes one revolution in
Substitute
Substitute
Therefore, the period of the tip of a one-link robot is
Substitute
Therefore, the frequency is
Since the one-link robot initially start form
Substitute
Here,
Substitute
The plot for the
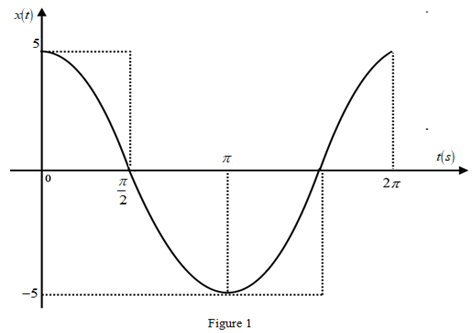
Substitute
Substitute
The plot for the
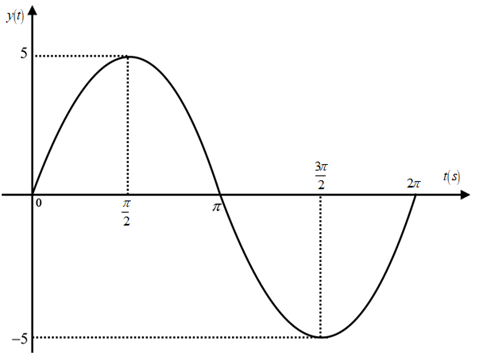
Figure 2
Substitute
Therefore, the time shift of the one-link robot is
The amplitude of sine and cosine function is
Conclusion:
Thus, the graph for
Want to see more full solutions like this?
Chapter 6 Solutions
Introductory Mathematics for Engineering Applications
Additional Math Textbook Solutions
Elementary Statistics: Picturing the World (7th Edition)
Calculus: Early Transcendentals (2nd Edition)
Elementary Statistics (13th Edition)
Introductory Statistics
Elementary Statistics
Thinking Mathematically (6th Edition)
- A sequence X = (xn) is said to be a contractive sequence if there is a constant 0 < C < 1 so that for all n = N. - |Xn+1 − xn| ≤ C|Xn — Xn−1| -arrow_forward3) Find the surface area of z -1≤ y ≤1 = 1 + x + y + x2 over the rectangle −2 ≤ x ≤ 1 and - Solution: TYPE YOUR SOLUTION HERE! ALSO: Generate a plot of the surface in Mathematica and include that plot in your solution!arrow_forward7. Walkabout. Does this graph have an Euler circuit? If so, find one. If not, explain why not.arrow_forward
- Below, let A, B, and C be sets. 1) Prove (AUB) nC = (ANC) U (BNC).arrow_forwardA sequence X = (xn) is said to be a contractive sequence if there is a constant 0 < C < 1 so that for all n = N. - |Xn+1 − xn| ≤ C|Xn — Xn−1| -arrow_forward1) Suppose continuous random variable X has sample space S = [1, ∞) and a pdf of the form f(x) = Ce-(2-1)/2. What is the expected value of X?arrow_forward
- Blue Ridge Hot Tubs manufactures and sells two models of hot tubs: the Aqua-Spa and the Hydro-Lux. Howie Jones, the owner and manager of the company, needs to decide how many of each type of hot tub to produce during his next production cycle. Howie buys prefabricated fiberglass hot tub shells from a local supplier and adds the pump and tubing to the shells to create his hot tubs. (This supplier has the capacity to deliver as many hot tub shells as Howie needs.) Howie installs the same type of pump into both hot tubs. He will have only 200 pumps available during his next production cycle. From a manufacturing standpoint, the main difference between the two models of hot tubs is the amount of tubing and labor required. Each Aqua-Spa requires 9 hours of labor and 12 feet of tubing. Each Hydro-Lux requires 6 hours of labor and 16 feet of tubing. Howie expects to have 1,566 production labor hours and 2,880 feet of tubing available during the next production cycle. Howie earns a profit of…arrow_forwardNo chatgpt pls will upvotearrow_forwardFind an nfa that accepts the language L(aa (a + b)). Create and test the NFA in Jflap. Test the strings: aab, ab, aaaa, aaaab, baab, aa, abbbb, a, b, 1. Submit the Jflap diagram and the Jflap test cases. 4. Find an nfa that accepts the language L (aa* (a+b)).arrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
