
a) Show that there are no critical points when c<√0.5, one critical point for c<√0.5, and two criticalpoints when c<√0.5.
b) Find the critical point(s) and determine the eigenvalues of the associated Jacobian matrix when c<√0.5 and when c=1.
c) How do you think trajectories of the system will behavefor c=1? Plot the trajectory starting at the origin. Does itbehave the way that you expected?
d) Choose one or two other initial points and plot the corresponding trajectories. Do these plots agree with your expectations?
(a)
To prove: There are no critical points for the system x'=−y−z, y'=x+ay, z'=b+z(x−c) where a=0.25, b=0.5 and c>0 when c<√0.5, one critical point for c=√0.5, and two critical points for c>√0.5.
Explanation of Solution
Given information:
The system of equations is x'=−y−z, y'=x+ay, z'=b+z(x−c).
Formula used:
Quadratic formula:
The roots of the equations ax2+bx+c=0 are x=−b±√b2−4ac2a.
Proof:
Consider x'=−y−z, y'=x+ay, z'=b+z(x−c)
By plugging a=0.25, b=0.5,
The system becomes x'=−y−z, y'=x+0.25y, z'=0.5+z(x−c)
The points, if any, where f(x) = 0 are called critical pointsof the autonomous system x' = f(x).
The critical points of the system x'=−y−z, y'=x+ay, z'=b+z(x−c) are found by solving the equations −y−z=0, x+0.25y=0 and 0.5+z(x−c)=0.
Consider the first equation −y−z=0.
⇒−y=z
Consider the second equation x+0.25y=0.
⇒x=−0.25y
Now plug these value in the equation 0.5+z(x−c)=0,
⇒0.5−y(−0.25y−c)=0
⇒0.5+0.25y2+cy=0
⇒0.25y2+cy+0.5=0
⇒y2+4cy+2=0
By using the quadratic formula,
⇒y=−4c±√16c2−82
⇒y=−2c±√2(2c2−1)
Thus the value of y is not real when 2c2−1<0.
That is, c<√0.5.
Thus there is no critical point when c<√0.5.
Also, there are two distinct real values of when 2c2−1>0.
That is, c>√0.5
Thus there are two critical points when c>√0.5.
If c=√0.5 that is 2c2−1=0 then we get a unique value of y.
Thus there is only one critical point for the system.
(b)
The critical points of the system x'=−y−z, y'=x+ay, z'=b+z(x−c) when c=√0.5 and c=1. Also, find the eigenvalues of the associated Jacobian matrix when c=√0.5 and c=1.
Answer to Problem 1P
Solution:
When c=√0.5 then thecritical point is (√24, −√2, √2) and eigenvalues of the corresponding linear system are 0, −0.0517767±1.52419i.
When c=1 then the critical points are (0.8536, −3.4142, 3.4142) and (0.1464, −0.5858, 0.5858). The corresponding eigenvalues of the linear system are −0.530252, −0.0366507±1.154204i and 0.161186, −0.0288165±2.094929i respectively.
Explanation of Solution
Given information:
The system is x'=−y−z, y'=x+ay, z'=b+z(x−c).
Explanation:
The system is x'=−y−z, y'=x+ay, z'=b+z(x−c).
By plugging a=0.25, b=0.5 and c=√0.5,
The system becomes, x'=−y−z, y'=x+0.25y, z'=0.5+z(x−√0.5).
From part (a),
The critical point is x=−0.25y, y=−2c±√2(2c2−1) and y=−z.
Hence if c=√0.5 then y=−2√0.5=−2√22=−√2.
Therefore, the critical point is (√24, −√2, √2).
Since F(x,y, z)=−y−z, G(x,y, z)= x+0.25y and H(x,y, z)= 0.5+z(x−√0.5), the Jacobian matrix is given by,
J(x,y, z)=(FxFyFzGxGyGzHxHyHz)=(0−1−110.250z0x−c)
i) Near the critical point (√24, −√2, √2), the Jacobian matrix becomes,
J(√24, −√2, √2)=(0−1−110.250√20√24−√22)
J(√24, −√2, √2)=(0−1−110.250√20−√24)
To find eigenvalues of the matrix (0−1−110.250√20−√24):
Let A=(0−1−110.250√20−√24) and the eigenvalues are λ1, λ2, λ3.
The characteristics equation is |A−λI|=0,
⇒|−λ−1−110.25−λ0√20−√24−λ|=0
⇒−λ(0.25−λ)((−√2/4)−λ)+((−√2/4)−λ)+√2(0.25−λ)=0
⇒−λ(14−λ)(−√24−λ)−√24−λ+√24−√2λ=0
⇒√2λ16+−√2λ24+λ24−λ3−λ−√2λ=0.
⇒−λ3+(1−√24)λ2+(√216−1−√2)λ=0
⇒λ[(1−√24)λ−λ2+(√216−1−√2)]=0
⇒λ=0, −0.0517767±1.52419i
Thus the eigenvalues when c=√0.5 are 0, −0.0517767±1.52419i.
The system is x'=−y−z, y'=x+ay, z'=b+z(x−c).
By plugging a=0.25, b=0.5 and c=1,
The system becomes, x'=−y−z, y'=x+0.25y, z'=0.5+z(x−1).
From part (a),
The critical point is x=−0.25y, y=−2c±√2(2c2−1) and y=−z.
Hence if c=1 then y=−2±√2.
That is, y=−2+√2 and y=−2−√2
Therefore, the critical points are (0.8536, −3.4142, 3.4142) and (0.1464, −0.5858, 0.5858).
Since F(x,y, z)=−y−z, G(x,y, z)= x+0.25y and H(x,y, z)= 0.5+z(x−1), the Jacobian matrix is given by,
J(x,y, z)=(FxFyFzGxGyGzHxHyHz)=(0−1−110.250z0x−1).
ii) Near the critical point (0.8536, −3.4142, 3.4142), the Jacobian matrix becomes,
J(0.8536, −3.4142, 3.4142)=(0−1−110.2503.414200.8536−1)
J(0.8536, −3.4142, 3.4142)=(0−1−110.2503.41420−0.1464)
To find eigenvalues of the matrix (0−1−110.2503.41420−0.1464):
Let A=(0−1−110.2503.41420−0.1464) and the eigenvalues are λ1, λ2, λ3.
The characteristics equation is |A−λI|=0,
⇒|−λ−1−110.25−λ03.41420−0.1464−λ|=0
⇒−λ(0.25−λ)(−0.1464−λ)+(−0.1464−λ)−3.4142(0.25−λ)=0
⇒0.0366λ+0.25λ2−0.1464λ2−λ3−0.1464−λ−0.8536+3.4142λ=0.
⇒0.1036λ2−λ3−1+2.4508λ=0
⇒−λ3+0.1036λ2+2.4508λ−1=0
⇒λ3−0.1036λ2−2.4508λ+1=0
⇒λ=0.161186, −0.0288165±2.094929i
iii) Near the critical point (0.1464, −0.5858, 0.5858), the Jacobian matrix becomes,
J(0.1464, −0.5858, 0.5858)=(0−1−110.2500.585800.1464−1)
J(0.1464, −0.5858, 0.5858)=(0−1−110.2500.58580−0.8536)
To find eigenvalues of the matrix (0−1−110.2500.58580−0.8536):
Let A=(0−1−110.2500.58580−0.8536) and the eigenvalues are λ1, λ2, λ3.
The characteristics equation is |A−λI|=0,
⇒|−λ−1−110.25−λ00.58580−0.8536−λ|=0
⇒−λ(0.25−λ)(−0.8536−λ)+(−0.8536−λ)+0.5858(0.25−λ)=0
⇒−0.8536(−0.25λ+λ2)−λ(−0.25λ+λ2)−0.8536−λ+0.1464−0.5858λ=0.
⇒0.2134λ−0.8536λ2+0.25λ2−λ3−0.8536−λ+0.1464−0.5858λ=0
⇒−0.6036λ2−λ3−0.7072−1.3724λ=0
⇒λ3+0.6036λ2+1.3724λ+0.7072=0
⇒λ=−0.530252, −0.0366507±1.154204i
Thus the eigenvalues when c=1 are −0.530252, −0.0366507±1.154204i and 0.161186, −0.0288165±2.094929i.
(c)
How the trajectories of the system will behave for c=1. Also, plot the trajectory starting at the origin. Whether it behave the way that you expected or not.
Answer to Problem 1P
Solution:
As t→∞ all solutions converge to the point (0.1464, −0.5858, 0.5858).
The trajectory starting at origin is:
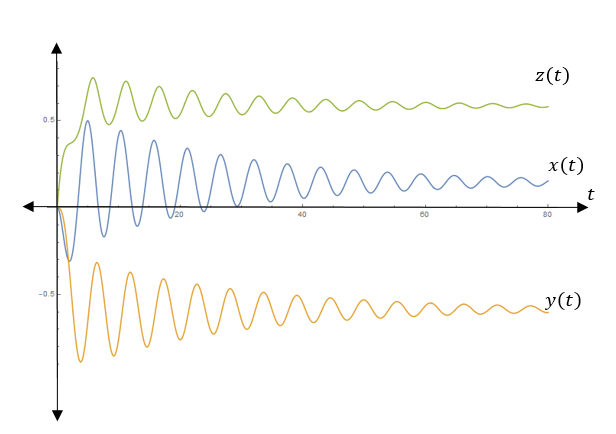
The graph is agreeing with our expectations.
Explanation of Solution
Given information:
The system is x'=−y−z, y'=x+ay, z'=b+z(x−c).
Explanation:
The system is x'=−y−z, y'=x+ay, z'=b+z(x−c).
From part (b),
The eigenvalues corresponding to the critical point (0.8536, −3.4142, 3.4142) are 0.161186, −0.0288165±2.094929i
Thus one of the eigenvalueshasa positive real part. Therefore, the critical point (0.8536, −3.4142, 3.4142) is unstable.
The eigenvalues corresponding to the critical point (0.1464, −0.5858, 0.5858) are −0.530252, −0.0366507±1.154204i
Thus the eigenvalues have a negative real part. Therefore, the critical point (0.1464, −0.5858, 0.5858) is stable which is asymptotically stable.
Therefore, as t→∞ all solutions converge to the point (0.1464, −0.5858, 0.5858).
The trajectory starting at the origin is:

As t→∞ all solutions converge to the point (0.1464, −0.5858, 0.5858)
Therefore, the graph is agreeing with our expectations.
(d)
To graph: The corresponding trajectories by choosing one or two initial points. Whether these plots agree with your expectations or not.
Explanation of Solution
Given information:
The system is x'=−y−z, y'=x+ay, z'=b+z(x−c) and c=1.
Graph:
The trajectory with the initial condition (0, 0, 0) is:

The trajectory with the initial condition (1, 1, 1) is:
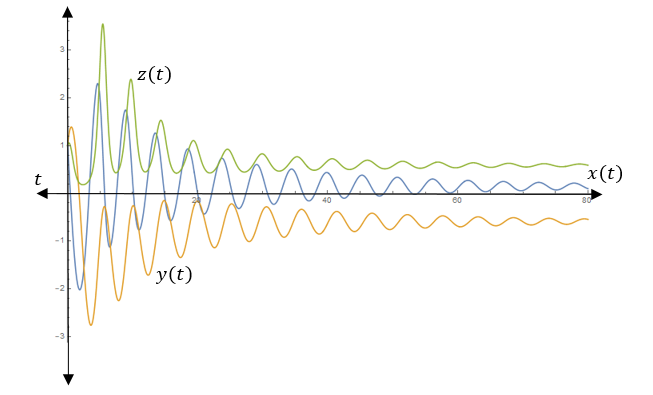
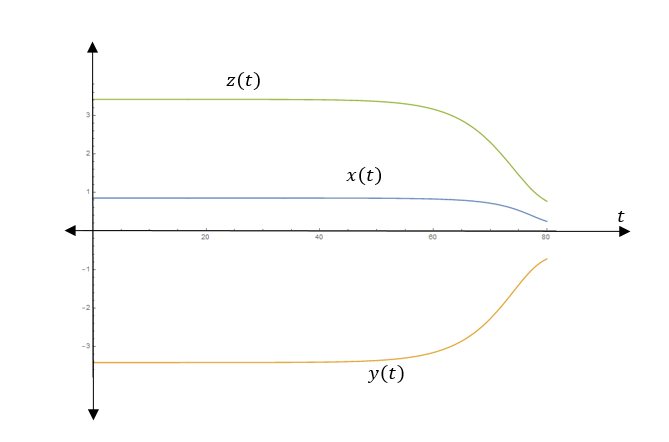
The trajectory with the initial point close to (0.8536, −3.4142, 3.4142) is:
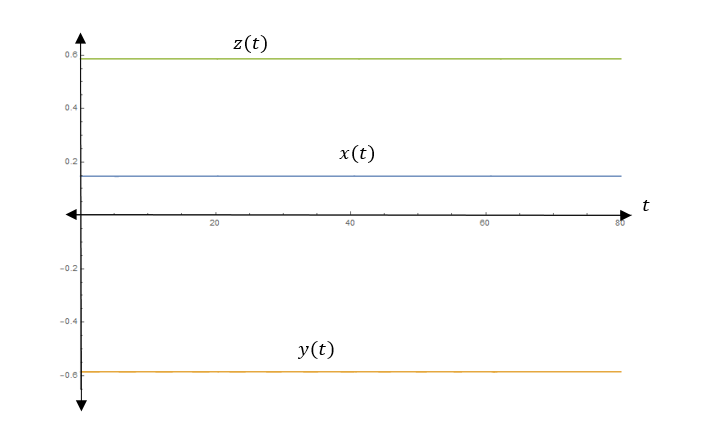
The trajectory with the initial point close to (0.1464, −0.5858, 0.5858) is:
Interpretation:
From the above graph,
All trajectories converge to the point (0.1464, −0.5858, 0.5858).
From part (c),
As t→∞ all solutions converge to the point (0.1464, −0.5858, 0.5858)
Therefore, the graph agrees with our expectations.
Want to see more full solutions like this?
Chapter 7 Solutions
Differential Equations: An Introduction to Modern Methods and Applications
Additional Math Textbook Solutions
Using and Understanding Mathematics: A Quantitative Reasoning Approach (6th Edition)
University Calculus: Early Transcendentals (4th Edition)
Elementary Statistics: Picturing the World (7th Edition)
Elementary Statistics
Algebra and Trigonometry (6th Edition)
A First Course in Probability (10th Edition)
- 7) 8) Let R be the region bounded by the given curves as shown in the figure. If the line x = k divides R into two regions of equal area, find the value of k 7. y = 3√x, y = √x and x = 4 8. y = -2, y = 3, x = −3, and x = −1 -1 2 +1 R Rarrow_forwardL sin 2x (1+ cos 3x) dx 59arrow_forwardConvert 101101₂ to base 10arrow_forward
- Definition: A topology on a set X is a collection T of subsets of X having the following properties. (1) Both the empty set and X itself are elements of T. (2) The union of an arbitrary collection of elements of T is an element of T. (3) The intersection of a finite number of elements of T is an element of T. A set X with a specified topology T is called a topological space. The subsets of X that are members of are called the open sets of the topological space.arrow_forward2) Prove that for all integers n > 1. dn 1 (2n)! 1 = dxn 1 - Ꮖ 4 n! (1-x)+/arrow_forwardDefinition: A topology on a set X is a collection T of subsets of X having the following properties. (1) Both the empty set and X itself are elements of T. (2) The union of an arbitrary collection of elements of T is an element of T. (3) The intersection of a finite number of elements of T is an element of T. A set X with a specified topology T is called a topological space. The subsets of X that are members of are called the open sets of the topological space.arrow_forward
- Definition: A topology on a set X is a collection T of subsets of X having the following properties. (1) Both the empty set and X itself are elements of T. (2) The union of an arbitrary collection of elements of T is an element of T. (3) The intersection of a finite number of elements of T is an element of T. A set X with a specified topology T is called a topological space. The subsets of X that are members of are called the open sets of the topological space.arrow_forward3) Let a1, a2, and a3 be arbitrary real numbers, and define an = 3an 13an-2 + An−3 for all integers n ≥ 4. Prove that an = 1 - - - - - 1 - - (n − 1)(n − 2)a3 − (n − 1)(n − 3)a2 + = (n − 2)(n − 3)aı for all integers n > 1.arrow_forwardDefinition: A topology on a set X is a collection T of subsets of X having the following properties. (1) Both the empty set and X itself are elements of T. (2) The union of an arbitrary collection of elements of T is an element of T. (3) The intersection of a finite number of elements of T is an element of T. A set X with a specified topology T is called a topological space. The subsets of X that are members of are called the open sets of the topological space.arrow_forward
- Definition: A topology on a set X is a collection T of subsets of X having the following properties. (1) Both the empty set and X itself are elements of T. (2) The union of an arbitrary collection of elements of T is an element of T. (3) The intersection of a finite number of elements of T is an element of T. A set X with a specified topology T is called a topological space. The subsets of X that are members of are called the open sets of the topological space.arrow_forwardDefinition: A topology on a set X is a collection T of subsets of X having the following properties. (1) Both the empty set and X itself are elements of T. (2) The union of an arbitrary collection of elements of T is an element of T. (3) The intersection of a finite number of elements of T is an element of T. A set X with a specified topology T is called a topological space. The subsets of X that are members of are called the open sets of the topological space.arrow_forward1) If f(x) = g¹ (g(x) + a) for some real number a and invertible function g, show that f(x) = (fo fo... 0 f)(x) = g¯¹ (g(x) +na) n times for all integers n ≥ 1.arrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning
Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning  College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning



