
Concept explainers
Landing Vehicle
NASA is planning a mission to Mars. To save money, engineers have decided to adapt one of the moon landing vehicles for the new mission. However, they are concerned about how the different gravitational forces will affect the suspension system that cushions the craft when it touches down. The acceleration resulting from gravity on the moon is 1.6 m/sec2, whereas on Mars it is 3.7 m/sec2.
The suspension system on the craft can be modeled as a damped spring mass system. In this case, the spring is below the moon lander, so the spring is slightly compressed at equilibrium, as shown in Figure 7.12.
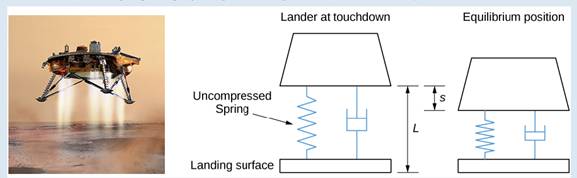
Figure 7.12 The landing craft suspension can be represented as a damped spring-mass system. (credit “lander": NASA)
We retain the convention that down is positive. Despite the new orientation, an examination of the forces affecting the lander shows that the same differential equation can be used to model the position of the landing craft relative to equilibrium:
where m is the mass of the lander, b is the damping coef?cient, and k is the spring constant.
1. The lander has a mass of 15,000 kg and the spring is 2 m long when uncompressed. The lander is designed to compress the spring 0.5 m to reach the equilibrium position under lunar gravity. The dashpot imparts a damping force equal to 48,000 times the instantaneous velocity of the lander. Set up the differential equation that models the motion of the lander when the craft lands on the moon.
Trending nowThis is a popular solution!

Chapter 7 Solutions
Calculus Volume 3
Additional Math Textbook Solutions
Calculus Volume 1
Calculus Volume 2
Introductory Statistics
Thinking Mathematically (6th Edition)
Mathematics for Elementary Teachers with Activities (5th Edition)
Calculus for Business, Economics, Life Sciences, and Social Sciences (13th Edition)
- Please see picturearrow_forwardSince there is no friction between the rod of mass M and length L and the plane, what will be the equation of motion of the falling rod? Note: C is the center of gravity and the gravitational acceleration is g. Barrow_forwardA mass weighting 64 lbs stretches a spring 3 inches. The mass is in a medium that exerts a damping force of 252 lbs when the mass has a speed of 6 ft/sec. Suppose the object is displaced an additional 7 inches and released. Find an equation for the object's displacement, u(t), in feet after t seconds. u(t) =arrow_forward
- A seasoned parachutist went for a skydiving trip where he performed freefall before deploying the parachute. According to Newton's Second Law of Motion, there are two forcës acting on the body of the parachutist, the forces of gravity (F,) and drag force due to air resistance (Fa) as shown in Figure 1. Fa = -cv ITM EUTM FUTM * UTM TM Fg= -mg x(t) UTM UT UTM /IM LTM UTM UTM TUIM UTM F UT GROUND Figure 1: Force acting on body of free-fall where x(t) is the position of the parachutist from the ground at given time, t is the time of fall calculated from the start of jump, m is the parachutist's mass, g is the gravitational acceleration, v is the velocity of the fall and c is the drag coefficient. The equation for the velocity and the position is given by the equations below: EUTM PUT v(t) = mg -et/m – 1) (Eq. 1.1) x(t) = x(0) – Where x(0) = 3200 m, m = 79.8 kg, g = 9.81m/s² and c = 6.6 kg/s. It was established that the critical position to deploy the parachutes is at 762 m from the ground…arrow_forwardBrazilian soccer star Marta has a penalty kick in the quarter-final match. She kicks the soccer ball from ground level with the (x, y)-coordinates (76, 21) on the soccer field shown in the figure and with initial velocity vo = 8i - 4j+23k ft/s. Assume an acceleration of 32 ft/s² due to gravity and that the goal net has a height of 8 ft and a total width of 24 ft. 105 ft 1 105 ft r₁ = rj = rk = 165 ft Determine the position function that gives the position of the ball t seconds after it is hit. (Use symbolic notation and fractions where needed.) r(t) = ri(t)i + rj(t)j + rk(t)k Incorrect 81+76 -41+21 ↓ 23r+1672² 165 ft 12 12arrow_forwardWrite Newton’s Second Law of Motion for three-dimensionalmotion with only the gravitational force (acting in the z-direction).arrow_forward
- Suppose a rock falls from rest from a height of 100 meters and the only force acting on it is gravity. Find an equation for the velocity v(t) as a function of time, measured in meters per second. Hint What is the initial velocity of the rock?arrow_forwardA ski jumper travels down a slope of the height H and leaves the ski track moving in the horizontal direction. The only force acting on the ski jumper is gravity. Find the height of the ski track h at which the ski jumper flies the longest distance.arrow_forwardA helicopter flies over the arctic ice pack at a constant altitude, towing an airborne 147-kg laser sensor which measures the thickness of the ice (see the drawing). The helicopter and the sensor move only in the horizontal direction and have a horizontal acceleration of magnitude 2.54 m/s2. Ignoring air resistance, find the tension in the cable towing the sensor.arrow_forward
- Use the concept of Particular Antiderivatives and Rectilinear Motion to answer the problem below: On the edge of an 8m building, Sam throws his toy vertically upwards at initial velocity = 28 m/s. If the only force that acts on the toy is accelerationdue to gravity (-32 ft/s), a. How many seconds will it take for the toy to reach its maximum height?b. What is the toy's speed when it hits the ground?arrow_forwardPlease answer immediately.arrow_forwardAn ant walks due east at a constant speed of 2 mi/hr on a sheet of paper that rests on a table. Suddenly, the sheet of paper starts moving due southeast at v2 mi/hr. The following is a correct solution for finding the resultant speed and direction of the ant relative to the table. Set up a coordinate system so that the positive y-axis corresponds to north and the positive x-axis corresponds to east. Then the velocity vector for the ant relative to the paper is given by (2,0). The velocity vector for the paper relative to the table is given by (v2 cos (-4), v2 sin (-5))= (1, –1). Therefore, the resultant velocity vector is given by (2,0) + (1, –1) = (3, –1). The speed of the ant relative to the table is v32 + 1² = v10 mi/hr and the direction the ant is traveling relative to the table is found by (금) using tan 0 = -1 where 0 represents the angle made with the positive r-axis. In this case 0 = arctan 3 3arrow_forward
 Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
