Chapter 7, Problem 1P

Consider the two-loop circuit shown in Fig P7.1. The currents $l_1$ and $l_2$ (in A) satisfy the following system of equations:

$16l_1-9l_2=110$ $(7.84)$ $20l_2-9l_1+110=0$ $(7.85)$

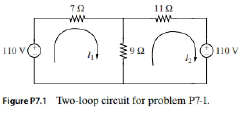
(a) Find $l_1$ and $l_2$ using the substitutions method.

(b) Write the system of equations $(7.84)$ and $(7.85)$ in the matrix form $AI=b$, where $I=\left[\begin{array}{c}{I}_1\\ I_2\end{array}\right]$.

(c) Find $l_1$ and $l_2$ using the matrix algebra method. Perform all computations by hand and show all steps.

(d) Find $l_1$ and $l_2$ using the Cramer’s rule.

To determine

(a)

The value of $I_1$ and $I_2$ using the substitution method.

Answer to Problem 1P

The value of $I_1$ is $5.06\text{ A}$ and $I_2$ is $-3.22\text{ A}$.

Explanation of Solution

Given:

The first system equation is:

  $16I_1-9I_2=110$ ..... (1)

The second system equation is:

  $20I_2-9I_1+110=0$ ..... (2)

Calculation:

Solve the system equation (1) for $I_1$

  $\begin{array}{c}16I_1-9I_2=110\\ 16I_1=110+9I_2\end{array}$

Simplify further.

$I_1=\frac{110+9I_2}{16}$ ..... (3)

Substitute $\frac{110+9I_2}{16}$ for $I_1$ in equation (2).

  $\begin{array}{c}20I_2-9\left(\frac{110+9I_2}{16}\right)+110=0\\ 20I_2-61.875-5.0625I_2+110=0\\ 14.9375I_2+48.125=0\end{array}$

Rearrange for $I_2$.

  $\begin{array}{c}14.9375I_2=-48.125\\ I_2=\frac{-48.125}{14.9375}\\ =-3.22\text{ A}\end{array}$

Substitute $-3.22\text{ A}$ for $I_2$ in equation (3).

  $\begin{array}{c}{I}_1=\frac{110+9\left(-3.22\right)}{16}\\ =5.06\text{ A}\end{array}$

Conclusion:

Thus, the value of $I_1$ is $5.06\text{ A}$ and $I_2$ is $-3.22\text{ A}$.

To determine

(b)

The system of equation in the form of $AI=b$ where $I=\left[\begin{array}{c}{I}_1\\ I_2\end{array}\right]$.

Answer to Problem 1P

The matrix form of the equation is $\left[\begin{array}{cc}16& -9\\ -9& 20\end{array}\right]\left[\begin{array}{c}{I}_1\\ I_2\end{array}\right]=\left[\begin{array}{c}110\\ -110\end{array}\right]$.

Explanation of Solution

Concept used:

The system of two simultaneous equations of variables in the form $a_{1}x+b_{1}y=c_1$ and $a_{2}x+b_{2}y=c_2$ can be written in the form of a matrix equation.

  $AX=b$ as follows:

  $\left[\begin{array}{cc}{a}_1& b_1\\ a_2& b_2\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]=\left[\begin{array}{c}{c}_1\\ c_2\end{array}\right]$

Here,

  $A=\left[\begin{array}{cc}{a}_1& b_1\\ a_2& b_2\end{array}\right]$ is the $2\times 2$ coefficient matrix.

  $X=\left[\begin{array}{c}x\\ y\end{array}\right]$ is the $2\times 1$ matrix of unknown variables and $b=\left[\begin{array}{c}{c}_1\\ c_2\end{array}\right]$ is the $2\times 1$ constant matrix on the right-hand side of the equation.

Calculation:

The system of equations represented by equation (1) and equation (2) can be written in the matrix form as follows:

  $\left[\begin{array}{cc}16& -9\\ -9& 20\end{array}\right]\left[\begin{array}{c}{I}_1\\ I_2\end{array}\right]=\left[\begin{array}{c}110\\ -110\end{array}\right]$

Conclusion:

Thus, the matrix form of the equation is $\left[\begin{array}{cc}16& -9\\ -9& 20\end{array}\right]\left[\begin{array}{c}{I}_1\\ I_2\end{array}\right]=\left[\begin{array}{c}110\\ -110\end{array}\right]$.

To determine

(c)

The value of $I_1$ and $I_2$ using the matrix algebra method.

Answer to Problem 1P

The value of $I_1$ is $5.06\text{ A}$ and $I_2$ is $-3.22\text{ A}$.

Explanation of Solution

Concept used:

Write the expression to calculate the value of the current using matrix method.

$I=A^{-1}b$ ...... (4)

Here, $A^{-1}$ is the inverse of the coefficient matrix $A$, $I$ is the matrix of unknown currents and $b$ is the coefficient matrix on the right-hand side of the equation.

Write the inverse of the matrix.

$A^{-1}=\frac{1}{\Delta }\left[adjA\right]$ ...... (5)

Here, $A$ is the coefficient matrix, $\Delta$ is the determinant of the matrix and $\left[adjA\right]$ is the adjoint of the matrix $A$.

Calculation:

The equation in the form $AI=b$ where $A=\left[\begin{array}{cc}16& -9\\ -9& 20\end{array}\right]$ is the $2\times 2$ coefficient matrix.

  $I=\left[\begin{array}{c}{I}_1\\ I_2\end{array}\right]$ is the $2\times 1$ matrix of unknown currents and $b=\left[\begin{array}{c}110\\ -110\end{array}\right]$ is the $2\times 1$ coefficient matrix on the right-hand side of the equation.

The determinant of matrix $A$ is given by:

  $\begin{array}{c}\Delta =\left|\begin{array}{cc}16& -9\\ -9& 20\end{array}\right|\\ =\left(16\right)\left(20\right)-\left(-9\right)\left(-9\right)\\ =320-81\\ =239\end{array}$

The adjoint of matrix $A$ is given by:

  $\left[adjA\right]=\left[\begin{array}{cc}20& 9\\ 9& 16\end{array}\right]$

Substitute $239$ for $\Delta$ and $\left[\begin{array}{cc}20& 9\\ 9& 16\end{array}\right]$ for $\left[adjA\right]$ in equation (5).

  $A^{-1}=\frac{1}{239}\left[\begin{array}{cc}20& 9\\ 9& 16\end{array}\right]$

Substitute $\frac{1}{239}\left[\begin{array}{cc}20& 9\\ 9& 16\end{array}\right]$ for $A^{-1}$, $\left[\begin{array}{c}{I}_1\\ I_2\end{array}\right]$ for $I$ and $\left[\begin{array}{c}110\\ -110\end{array}\right]$ for $b$ in equation (4).

  $\begin{array}{c} \left[\begin{array}{c}{I}_1\\ I_2\end{array}\right]=\frac{1}{239}\left[\begin{array}{cc}20& 9\\ 9& 16\end{array}\right]\left[\begin{array}{c}110\\ -110\end{array}\right]\\ =\frac{1}{239}\left[\begin{array}{c}2200-990\\ 990-1760\end{array}\right]\\ =\frac{1}{239}\left[\begin{array}{c}1210\\ -770\end{array}\right]\\ =\left[\begin{array}{c}5.06\\ -3.22\end{array}\right]\end{array}$

Conclusion:

Thus, the value of $I_1$ is $5.06\text{ A}$ and $I_2$ is $-3.22\text{ A}$.

To determine

(d)

The value of $I_1$ and $I_2$ using the matrix using Cramer's rule.

Answer to Problem 1P

The value of $I_1$ is $5.06\text{ A}$ and $I_2$ is $-3.22\text{ A}$.

Explanation of Solution

Concept used:

Write the expression for $I_1$ using Cramer's rule.

  $I_1=\frac{\left|\begin{array}{cc}{b}_1& a_{12}\\ b_2& a_{22}\end{array}\right|}{\left|A\right|}$ ...... (6)

Here, $I_1$ is the one solution of the equation and $\left|A\right|$ is the determinant of the matrix.

Write the expression for $I_2$ using Cramer's rule.

  $I_2=\frac{\left|\begin{array}{cc}{a}_{11}& b_1\\ a_{21}& b_2\end{array}\right|}{\left|A\right|}$ ...... (7)

Here, $I_2$ is the other solution of the equation.

Calculation:

Substitute $110$ for $b_1$, $-110$ for $b_2$, $-9$ for $a_{12}$, $20$ for $a_{22}$ and $239$ for $\left|A\right|$ in equation (6).

  $\begin{array}{c}{I}_1=\frac{\left|\begin{array}{cc}110& -9\\ -110& 20\end{array}\right|}{239}\\ =\frac{\left(2200-990\right)}{239}\\ =\frac{1210}{239}\\ =5.06\text{ A}\end{array}$

Substitute $110$ for $b_1$, $-110$ for $b_2$, $16$ for $a_{11}$, $-9$ for $a_{21}$ and $239$ for $\left|A\right|$ in equation (7).

  $\begin{array}{c}{I}_2=\frac{\left|\begin{array}{cc}16& 110\\ -9& -110\end{array}\right|}{239}\\ =\frac{\left(-1760+990\right)}{239}\\ =\frac{770}{239}\\ =3.22\text{ A}\end{array}$

Conclusion:

Thus, the value of $I_1$ is $5.06\text{ A}$ and $I_2$ is $-3.22\text{ A}$.