
Calculus: Early Transcendentals
8th Edition
ISBN: 9781285741550
Author: James Stewart
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Question
The logistic equation models the growth of a population. Use the equation to (a) find the value of k, (b) find the carrying capacity, (c) find the initial population, (d) determine when the population will
reach 50% of its carrying capacity, and (e) write a logistic
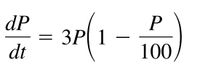
Transcribed Image Text:dP
3P 1
dt
100
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps with 3 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- Hello! How do you solve part (a), (b), and (c) of the question attached below? Thank you for your help! Have a nice day :)arrow_forwardAssume there is a certain population of fish in a pond whose growth is described by the logistic equation. The growth parameter for this type of fish is r = 3.0. The logistic growth formula is given by PN+1 rPN(1-PN) If originally the pond is stocked to 50% of its carrying capacity, then the population of the pond after the second breeding season is Select one: a. 25% of the pond's carrying capacity. b. 56.25% of the pond's carrying capacity. c. 75% of the pond's carrying capacity. d. none of these O e. 50% of the pond's carrying capacity.arrow_forwardA colony of 120 wood frogs was introduced to a pond with a carrying capacity of C=300. The population grows according to the logistic growth model, with a growth parameter is r = 1.5. The logistic growth formula is: pN+1 = rpN(1-pN) a) Find the initial p-value: p0 = Answer b) Find the first p-value: p1 = Answer c) Find the second p-value: p2 = Answerarrow_forward
- Biologists stocked a lake with 300 fish and estimated the carrying capacity (the maximal population for the fish of that species in that lake) to be 5000. The number of fish tripled in the first year. (a) Assuming that the size of the fish population satisfies the logistic equation dP = kp (1-P). (1-²), kP dt determine the constant k, and then solve the equation to find an expression for the size of the population after t years. k= P(t)= (b) How long will it take for the population to increase to 2500 (half of the carrying capacity)? It will take years.arrow_forwardPls do fast handwrittenarrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning

Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning