College Physics
1st Edition
ISBN: 9781938168000
Author: Paul Peter Urone, Roger Hinrichs
Publisher: OpenStax College
expand_more
expand_more
format_list_bulleted
Concept explainers
Textbook Question
thumb_up100%
Chapter 6, Problem 43PE
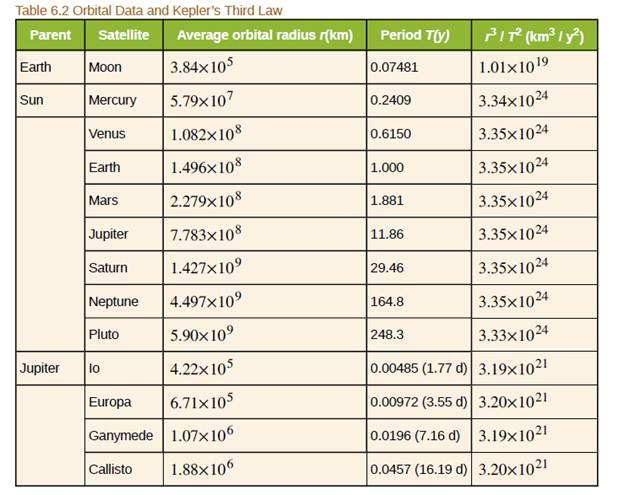
A geosynchronous Earth satellite is one that has an orbital period of precisely 1 day. Such orbits are useful for communication and weather observation because the satellite remains above the same point on Earth (provided it orbits in the equatorial plane in the same direction as Earth's rotation). Calculate the radius of such an orbit based on the data for the moon in Table 6.2
Expert Solution & Answer
Trending nowThis is a popular solution!
Students have asked these similar questions
A 3000-kg satellite orbits the Earth in a circular orbit 11797 km above the Earth's
surface (Earth radius = 6380 km, Earth Mass = 5.97x1024 kg).
What is the gravitational force (in newtons, N) between the satellite and the Earth?
Hint: The radius of the Earth + the height of the orbit = the center-to-center distance needed
for the equation. You also need the universal gravitational constant (G), which is not 9.81
m/s2. Be careful.
Gmim2
F
A geosynchronous Earth satellite is one that has an orbital period of precisely 1 day. Such orbits are useful for communication and weather observation because the satellite remains above the same point on Earth (provided it orbits in the equatorial plane in the same direction as Earth's rotation). Calculate the radius (in km) of such an orbit based on the data for the moon in this table.
A geosynchronous Earth satellite is one that has an orbital period of precisely 1 day. Such orbits are useful for communication and weather observation because the satellite remains above the same point on Earth (provided it orbits in the equatorial plane in the same direction as Earth’s rotation). Calculate the radius of such an orbit based on the data for the moon in Table.
Chapter 6 Solutions
College Physics
Ch. 6 - There an analogy between rotational and physical...Ch. 6 - Can centripetal acceleration change the speed of...Ch. 6 - If you wish to reduce the stress (which related to...Ch. 6 - Define centripetal force. Can any type of force...Ch. 6 - If centripetal force is directed toward the...Ch. 6 - Pace car drivers routinely cut corners as shown in...Ch. 6 - A number of amusement parks have rides that make...Ch. 6 - What is the direction of the force exerted by the...Ch. 6 - As a skater forms a circle, what force is...Ch. 6 - Suppose a child is riding on a merry-go-round at a...
Ch. 6 - Do you feel yourself thrown to either side when...Ch. 6 - Suppose a mass is moving in a circular path on a...Ch. 6 - When a toilet is flushed or a sink is drained,...Ch. 6 - Is there a real force that throws water from...Ch. 6 - In one amusement park ride, riders enter a large...Ch. 6 - Actin at a distance, such as is the case for...Ch. 6 - Two friends are having a conversation. Anna says a...Ch. 6 - A frame of reference placed at the center of the...Ch. 6 - Action at a distance, such as is the case for...Ch. 6 - Two friends are having a conversation. Anna says a...Ch. 6 - Draw a free body diagram for a satellite in an...Ch. 6 - Newton's laws of motion and gravity were among the...Ch. 6 - In what frame(s) of reference are Kepler's laws...Ch. 6 - Semi-trailer trucks have an odometer on one hub of...Ch. 6 - Microwave ovens rotate at a rate of about 6...Ch. 6 - An automobile with 0.260 m radius tires travels...Ch. 6 - (a) What is the period of rotation of Earth in...Ch. 6 - A baseball pitcher brings his arm forward during a...Ch. 6 - In lacrosse, a ball is thrown from a net on the...Ch. 6 - A truck with 0.420-m-radius tires travels at 32.0...Ch. 6 - Integrated Concepts When kicking a football, the...Ch. 6 - Construct Your Own Problem Consider an amusement...Ch. 6 - A fairground ride spins its occupants inside a...Ch. 6 - A runner taking part in the 200 m dash must run...Ch. 6 - Taking the age of Earth to be about 4109 years and...Ch. 6 - The propeller of a World War Il fighter plane is...Ch. 6 - An ordinary workshop grindstone has a radius of...Ch. 6 - Helicopter blades withstand tremendous stresses....Ch. 6 - Olympic ice skaters are able to spin at about 5...Ch. 6 - What percentage of the acceleration at Earth's...Ch. 6 - Verify that the linear speed of an ultracentrifuge...Ch. 6 - A rotating space station is said to create...Ch. 6 - At takeoff, a commercial jet has a 60.0 m/s speed....Ch. 6 - Integrated Concepts Riders in an amusement park...Ch. 6 - Unreasonable Results A mother pushes her child on...Ch. 6 - (a) A 22.0 kg child is riding a playground...Ch. 6 - Calculate the centripetal force on the end of a...Ch. 6 - What is the ideal banking angle for a gentle turn...Ch. 6 - What is the ideal speed to take a 100 m radius...Ch. 6 - (a) What is the radius of a bobsled turn banked at...Ch. 6 - Part of riding a bicycle involves leaning at the...Ch. 6 - A large centrifuge, like the one shown in Figure...Ch. 6 - Integrated Concepts If a car takes a banked curve...Ch. 6 - Modern roller coasters have vertical loops like...Ch. 6 - Unreasonable Results (a) Calculate the minimum...Ch. 6 - (a) Calculate Earth's mass given the acceleration...Ch. 6 - (a) Calculate the magnitude of the acceleration...Ch. 6 - (a) What is the acceleration due to gravity on the...Ch. 6 - (a) Calculate the acceleration due to gravity on...Ch. 6 - The Moon and Earth rotate about their common...Ch. 6 - Solve part (b) of Example 6.6 using ac=v2/r.Ch. 6 - Astrology, that unlikely and vague pseudoscience,...Ch. 6 - The existence of the dwarf planet Pluto was...Ch. 6 - (a) The Sun orbits the Milky Way galaxy once each...Ch. 6 - Unreasonable Result A mountain 10.0 km from a...Ch. 6 - A geosynchronous Earth satellite is one that has...Ch. 6 - Calculate the mass of the Sun based on data for...Ch. 6 - Find the mass of Jupiter based on data for the...Ch. 6 - Find the ratio of the mass of Jupiter to that of...Ch. 6 - Astronomical observations of our Milky Way galaxy...Ch. 6 - Integrated Concepts Space debris left from old...Ch. 6 - Unreasonable Results (a) Based on Kepler's laws...Ch. 6 - Construct Your Own Problem On February 14, 2000,...
Additional Science Textbook Solutions
Find more solutions based on key concepts
How does the net work done on cart A(Wnet,A) compare to the net work done on cart B(Wnet,B) ? Explain. Is the k...
Tutorials in Introductory Physics
The pV-diagram of the Carnot cycle.
Sears And Zemansky's University Physics With Modern Physics
Two hundred joules of heat are removed from a heat at a temperature of 200 K. What is the entropy change of the...
University Physics Volume 2
The force, when you push against a wall with your fingers, they bend.
Conceptual Physics (12th Edition)
41. A hollow metal sphere has 6 cm and 10 cm inner and outer radii, respectively. The surface charge density on...
Physics for Scientists and Engineers: A Strategic Approach, Vol. 1 (Chs 1-21) (4th Edition)
41. A 0.300 kg oscillator has a speed of 95.4cm/s when its displacement is 3.00cm and 71.4 cm/s when its displ...
Physics for Scientists and Engineers: A Strategic Approach with Modern Physics (4th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- Calculate the effective gravitational field vector g at Earths surface at the poles and the equator. Take account of the difference in the equatorial (6378 km) and polar (6357 km) radius as well as the centrifugal force. How well does the result agree with the difference calculated with the result g = 9.780356[1 + 0.0052885 sin 2 0.0000059 sin2(2)]m/s2 where is the latitude?arrow_forwardSuppose the gravitational acceleration at the surface of a certain moon A of Jupiter is 2 m/s2. Moon B has twice the mass and twice the radius of moon A. What is the gravitational acceleration at its surface? Neglect the gravitational acceleration due to Jupiter, (a) 8 m/s2 (b) 4 m/s2 (c) 2 m/s2 (d) 1 m/s2 (e) 0.5 m/s2arrow_forwardWhat is the orbital radius of an Earth satellite having a period of 1.00 h? (b) What is unreasonable about this result?arrow_forward
- Let gM represent the difference in the gravitational fields produced by the Moon at the points on the Earths surface nearest to and farthest from the Moon. Find the fraction gM/g, where g is the Earths gravitational field. (This difference is responsible for the occurrence of the lunar tides on the Earth.)arrow_forwardA planet has two moons of equal mass. Moon 1 is in a circular orbit of radius r. Moon 2 is in a circular orbit of radius 2r. What is the magnitude of the gravitational force exerted by the planet on Moon 2? (a) four times as large as that on Moon 1 (b) twice as large as that on Moon 1 (c) equal to that on Moon 1 (d) half as large as that on Moon 1 (e) one-fourth as large as that on Moon 1arrow_forwardIt was stated that a satellite with negative total energy is in a bound orbit, whereas one with zero or positive total energy is in an unbounded orbit. Why zero or positive total energy is in an unbounded orbit. Why is this true? What choice for gravitational potential energy was made such that this is true?arrow_forward
- On a planet whose radius is 1.2107m , the acceleration due to gravity is 18m/s2 . What is the mass of the planet?arrow_forwardWhat is the orbital period of a satellite orbiting just above the surface of the asteroid in Problem 11?arrow_forward(a) Based on the observations, determine the total mass M of the planet. (b) Which moon and planet of our solar system is the team observing? (Use literature.)arrow_forward
- A satellite placed in a geostationary orbit will orbit with the Earth's rotation (every 24 hours), meaning that the satellite can remain directly above the same ground location. Communication and weather monitoring satellites are often placed in geostationary orbits to maintain contact with ground based towers or observation areas. What is the orbital radius of a geostationary satellite? (Give your answer in thousands of km.) Mass of Earth: 5.98x1024 kg. Note: This is over 3 times the diameter of the earth.arrow_forwardA geosynchronous orbit for a satellite is a circular orbit about the equator of the Earth in which the satellite stays fixed over a point on the equator. Use the fact that the Earth makes one revolution about its axis every 24 hours to find the altitude in miles of a communications satellite in geosynchronous orbit. Assume the Earth to be a sphere of radius 4000 mi.arrow_forwardA satellite orbits a planet in a circular orbit at an altitude (distance above the surface) of 1000km. The radius of the planet is 8000 km. The mass of the planet is 8 x 10^24 kg. What is the orbital speed? Your answer The gravitational force between a planet and its moon is óx10^16 N. For another moon orbiting the same planet with twice the orbital radius and 3 times the 5.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based Text
Physics
ISBN:9781133104261
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...
Physics
ISBN:9781133939146
Author:Katz, Debora M.
Publisher:Cengage Learning
University Physics Volume 1
Physics
ISBN:9781938168277
Author:William Moebs, Samuel J. Ling, Jeff Sanny
Publisher:OpenStax - Rice University
Glencoe Physics: Principles and Problems, Student...
Physics
ISBN:9780078807213
Author:Paul W. Zitzewitz
Publisher:Glencoe/McGraw-Hill
Classical Dynamics of Particles and Systems
Physics
ISBN:9780534408961
Author:Stephen T. Thornton, Jerry B. Marion
Publisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...
Physics
ISBN:9781305116399
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning