
Concept explainers
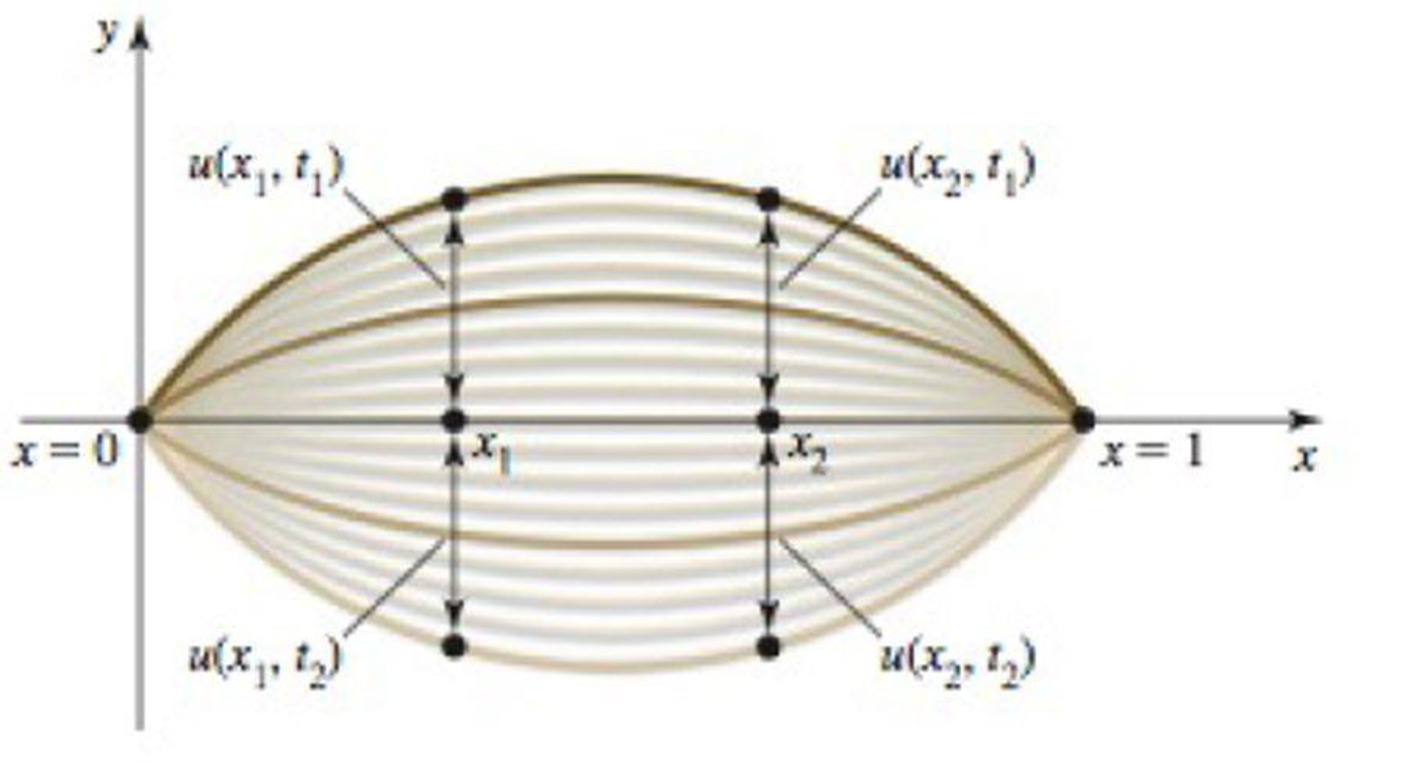
Wave on a string Imagine a string that is fixed at both ends (for example, a guitar string). When plucked, the string forms a standing wave. The displacement u of the string varies with position x and with time t. Suppose it is given by u = f(x, t) = 2 sin (πx) sin (πt/2), for 0 ≤ x ≤ 1 and t ≥ 0 (see figure). At a fixed point in time, the string forms a wave on [0, 1]. Alternatively, if you focus on a point on the string (fix a value of x), that point oscillates up and down in time.
a. What is the period of the motion in time?
b. Find the rate of change of the displacement with respect to time at a constant position (which is the vertical velocity of a point on the string).
c. At a fixed time, what point on the string is moving fastest?
d. At a fixed position on the string, when is the string moving fastest?
e. Find the rate of change of the displacement with respect to position at a constant time (which is the slope of the string).
f. At a fixed time, where is the slope of the string greatest?
Trending nowThis is a popular solution!

Chapter 15 Solutions
Calculus: Early Transcendentals (3rd Edition)
Additional Math Textbook Solutions
Precalculus Enhanced with Graphing Utilities (7th Edition)
Calculus, Single Variable: Early Transcendentals (3rd Edition)
Glencoe Math Accelerated, Student Edition
University Calculus: Early Transcendentals (4th Edition)
Calculus and Its Applications (11th Edition)
Precalculus (10th Edition)
 Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage LearningAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage LearningAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage

