EBK PRACTICE OF STAT.F/AP EXAM,UPDATED
6th Edition
ISBN: 9781319287573
Author: Starnes
Publisher: MPS PUB
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Question
Chapter 1.2, Problem 50E
To determine
Discuss the shape of the distribution.
Expert Solution & Answer
Answer to Problem 50E
The shape is roughly symmetric with single peak and having no gaps.
Explanation of Solution
Given information:
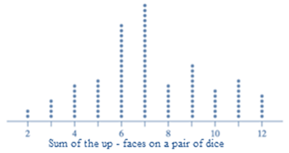
Since,
The peak in the dotplot roughly lies in the middle of the graph.
Thus,
The distribution is roughly symmetric.
Note that
The single peak of the distribution lies at 7.
However,
In the dotplot, there appear to be no gaps.
Thus,
The shape is roughly symmetric with single peak and no gaps.
Chapter 1 Solutions
EBK PRACTICE OF STAT.F/AP EXAM,UPDATED
Ch. 1.1 - Prob. 11ECh. 1.1 - Prob. 12ECh. 1.1 - Prob. 13ECh. 1.1 - Prob. 14ECh. 1.1 - Prob. 15ECh. 1.1 - Prob. 16ECh. 1.1 - Prob. 17ECh. 1.1 - Prob. 18ECh. 1.1 - Prob. 19ECh. 1.1 - Prob. 20E
Ch. 1.1 - Prob. 21ECh. 1.1 - Prob. 22ECh. 1.1 - Prob. 23ECh. 1.1 - Prob. 24ECh. 1.1 - Prob. 25ECh. 1.1 - Prob. 26ECh. 1.1 - Prob. 27ECh. 1.1 - Prob. 28ECh. 1.1 - Prob. 29ECh. 1.1 - Prob. 30ECh. 1.1 - Prob. 31ECh. 1.1 - Prob. 32ECh. 1.1 - Prob. 33ECh. 1.1 - Prob. 34ECh. 1.1 - Prob. 35ECh. 1.1 - Prob. 36ECh. 1.1 - Prob. 37ECh. 1.1 - Prob. 38ECh. 1.1 - Prob. 39ECh. 1.1 - Prob. 40ECh. 1.1 - Prob. 41ECh. 1.1 - Prob. 42ECh. 1.1 - Prob. 43ECh. 1.1 - Prob. 44ECh. 1.2 - Prob. 45ECh. 1.2 - Prob. 46ECh. 1.2 - Prob. 47ECh. 1.2 - Prob. 48ECh. 1.2 - Prob. 49ECh. 1.2 - Prob. 50ECh. 1.2 - Prob. 51ECh. 1.2 - Prob. 52ECh. 1.2 - Prob. 53ECh. 1.2 - Prob. 54ECh. 1.2 - Prob. 55ECh. 1.2 - Prob. 56ECh. 1.2 - Prob. 57ECh. 1.2 - Prob. 58ECh. 1.2 - Prob. 59ECh. 1.2 - Prob. 60ECh. 1.2 - Prob. 61ECh. 1.2 - Prob. 62ECh. 1.2 - Prob. 63ECh. 1.2 - Prob. 64ECh. 1.2 - Prob. 65ECh. 1.2 - Prob. 66ECh. 1.2 - Prob. 67ECh. 1.2 - Prob. 68ECh. 1.2 - Prob. 69ECh. 1.2 - Prob. 70ECh. 1.2 - Prob. 71ECh. 1.2 - Prob. 72ECh. 1.2 - Prob. 73ECh. 1.2 - Prob. 74ECh. 1.2 - Prob. 75ECh. 1.2 - Prob. 76ECh. 1.2 - Prob. 77ECh. 1.2 - Prob. 78ECh. 1.2 - Prob. 79ECh. 1.2 - Prob. 80ECh. 1.2 - Prob. 81ECh. 1.2 - Prob. 82ECh. 1.2 - Prob. 83ECh. 1.2 - Prob. 84ECh. 1.2 - Prob. 85ECh. 1.2 - Prob. 86ECh. 1.3 - Prob. 87ECh. 1.3 - Prob. 88ECh. 1.3 - Prob. 89ECh. 1.3 - Prob. 90ECh. 1.3 - Prob. 91ECh. 1.3 - Prob. 92ECh. 1.3 - Prob. 93ECh. 1.3 - Prob. 94ECh. 1.3 - Prob. 95ECh. 1.3 - Prob. 96ECh. 1.3 - Prob. 97ECh. 1.3 - Prob. 98ECh. 1.3 - Prob. 99ECh. 1.3 - Prob. 100ECh. 1.3 - Prob. 101ECh. 1.3 - Prob. 102ECh. 1.3 - Prob. 103ECh. 1.3 - Prob. 104ECh. 1.3 - Prob. 105ECh. 1.3 - Prob. 106ECh. 1.3 - Prob. 107ECh. 1.3 - Prob. 108ECh. 1.3 - Prob. 109ECh. 1.3 - Prob. 110ECh. 1.3 - Prob. 111ECh. 1.3 - Prob. 112ECh. 1.3 - Prob. 113ECh. 1.3 - Prob. 114ECh. 1.3 - Prob. 115ECh. 1.3 - Prob. 116ECh. 1.3 - Prob. 117ECh. 1.3 - Prob. 118ECh. 1.3 - Prob. 119ECh. 1.3 - Prob. 120ECh. 1.3 - Prob. 121ECh. 1.3 - Prob. 122ECh. 1.3 - Prob. 123ECh. 1.3 - Prob. 124ECh. 1.3 - Prob. 125ECh. 1.3 - Prob. 126ECh. 1.3 - Prob. 127ECh. 1.3 - Prob. 128ECh. 1 - Prob. 1ECh. 1 - Prob. 2ECh. 1 - Prob. 3ECh. 1 - Prob. 4ECh. 1 - Prob. 5ECh. 1 - Prob. 6ECh. 1 - Prob. 7ECh. 1 - Prob. 8ECh. 1 - Prob. 9ECh. 1 - Prob. 10ECh. 1 - Prob. R1.1RECh. 1 - Prob. R1.2RECh. 1 - Prob. R1.3RECh. 1 - Prob. R1.4RECh. 1 - Prob. R1.5RECh. 1 - Prob. R1.6RECh. 1 - Prob. R1.7RECh. 1 - Prob. R1.8RECh. 1 - Prob. R1.9RECh. 1 - Prob. R1.10RECh. 1 - Prob. T1.1SPTCh. 1 - Prob. T1.2SPTCh. 1 - Prob. T1.3SPTCh. 1 - Prob. T1.4SPTCh. 1 - Prob. T1.5SPTCh. 1 - Prob. T1.6SPTCh. 1 - Prob. T1.7SPTCh. 1 - Prob. T1.8SPTCh. 1 - Prob. T1.9SPTCh. 1 - Prob. T1.10SPTCh. 1 - Prob. T1.11SPTCh. 1 - Prob. T1.12SPTCh. 1 - Prob. T1.13SPTCh. 1 - Prob. T1.14SPT
Additional Math Textbook Solutions
Find more solutions based on key concepts
Sampling Method. In Exercises 9-12, determine whether the sampling method appears to be sound or is flawed.
9. ...
Elementary Statistics
Two fair dice are rolled. What is the conditional probability that at least one lands on 6 given that the dice ...
A First Course in Probability (10th Edition)
In track, the second lane from the inside of the track is longer than the inside lane. Use this information to ...
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
The equivalent expression of x(y+z) by using the commutative property.
Calculus for Business, Economics, Life Sciences, and Social Sciences (14th Edition)
Use the Integral Test to determine whether the series in Exercises 1–12 converge or diverge. Be sure to check t...
University Calculus: Early Transcendentals (4th Edition)
1. Distributions Using the methods of this chapter, identify the distribution that should be used for testing a...
Elementary Statistics (13th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, statistics and related others by exploring similar questions and additional content below.Similar questions
- 15.15. A product is shipped in lots of size N = 2,000. Find a Dodge-Romig single-sampling plan for which the LTPD = 1%, assuming that the process average is 0.25% defective. Draw the OC curve and the ATI curve for this plan. What is the AOQL for this sampling plan? The sampling plan that should be used is n = 490 and c = 4. If rejected lots are screened 100% and defective items replaced with good ones, the AOQL (from Table 15.9) is approximately X.XX%. n: from Table 15.9 c: from Table 15.9 Dodge-Romig, LTPD=1.0%, N=2000, process avg = 0.25% N= 2000 n= from Table 15.9 C= from Table 15.9 р D=N*p Pa ATI AOQ 0.001 0.002 ---- 0.020 OC curve for N=2000, n=, c=, AOQL= % ATI curve for N=2000, n= C=arrow_forward15.8. Consider the single-sampling plan found in Exercise 15.5. Suppose that lots of N = 2,000 are submitted. Draw the ATI curve for this plan. Draw the AOQ curve and find the AOQL. n = 35; c = 1; N = 2,000 ATI = n + (1 − Pa)(N − n) Pap(N-n) AOQ AOQL N N= n= C= 2000 35 1 P binomial Pa=Pr{d<=1} ATI AOQ 0.001 0.999 36 0.0010 0.002 0.998 39 0.0020 0.003 0.995 45 0.0029 0.004 0.991 52 0.0039 ATI curve for n=35, c=1| AOQ curve for n-35, c=1arrow_forwardProblem 2: (10 pts) You have observations on investments (y) and profits (x) for 100 civil engineering firms. You assume that you can fit a linear regression model using OLS as follows: y=a+ẞX + ε You want to obtain estimates for a and B. a) Suppose every civil engineering firm in the sample has the same amount of profits. What, if any, problem would this create? Explain and justify your answer. b) If the distribution of the profits were not normal, can you use linear regression? Explain and justify your answer. c) If profits were presented in categories, would estimating a linear regression model be appropriate? Explain and justify your answer.arrow_forward
- All analysis, calculations, and explanations must be done in a single Excel file (use separate Excel sheets for each question). Upload the completed Excel file using the file extension format Lastname_Firstname_RegressionProblem. Regression Problem Sarah Anderson, the business analyst at TV Revolution, is conducting research on the dealership’s various television brands. She has collected data over the past year (2022) on the manufacturer, screen size, and price of various television brands. The data is given in the file below. You have been hired as an intern to run analyses on the data and report the results back to Sarah; the five questions that Sarah needs you to address are given below. Does there appear to be a positive or negative relationship between price and screen size? Use a scatter plot to examine the relationship. Determine and interpret the correlation coefficient between the two variables. In your interpretation, discuss the direction of the relationship (positive,…arrow_forwardQuestion number 6 (4 points) Sampling assignment: A list of the top 100 universities in the world is provided in the attached file. Draw a sample of 40 universities using random sampling and include a snapshot of your results from Excel in this Microsoft Word file (2 points: 1 for generating random numbers and the other for the sample drawn from the dataset.) Draw a sample of 20 universities using systematic sampling. Make sure to randomize the data before systematic sampling; and include a snapshot from Microsoft Excel in this Microsoft Word file (2 points). You can use the following template for systematic sampling.arrow_forwardThe data provided in the following table pertains to three separate questions: One sample T-test, Two Sample T-Test, and ANOVA. The same data is also provided in Microsoft Excel file. Answer the questions provided in the table. Report your results by comparing the significance level to 5%. Additionally, state your conclusion clearly in terms of whether the null hypothesis is rejected or not rejected. Avoid using terms like "accepted" or "not accepted" in your conclusion. Question 1: A retail store manager claims that the average daily sales of the store are $1,500. You aim to test whether the actual average daily sales differ significantly from this claimed value. (2 points = 0.25x4 parts) Make null and alternative hypothesis for one sample T-test Conduct One Sample T Test and provide a snapshot of results from excel. Null = Alternative = Conclusion: Since the p value is (choose one: less / greater) than 5%,arrow_forward
- 6. We are trying to model the relationship between X = the amount of for tilizer (tons per acre), and Y = corn yield (tone per acre). The following data were obtained for n=6 experimental plots y ** y* *y 0 18 0 324 0 1 22 1 484 7 2 24 4 576 48 3 25 7 625 75 4 25 16 625 100 Total 10 114 ? 2634 245 19 20 y 21 22 23 24 25 22 23 18 (a) Compute the regression equation of Y as a linear function of X. Add the regression line to the plot. (b) Predict the yield when X = 0.1. (c) Find the value of the correlation coefficient. Extra Credit Conduct a hypothesis test of whether the correlation is significantly different from 0.arrow_forwardThe data below provides the length (in inches) of 17 fish caught by guests on Tammy’s Charter Fishing Boat this weekend. Calculate the upper fence to determine if the largest fish caught that day was an outlier. NOTE: Upper fence = Q3 + 1.5 (IQR) and calculator use is allowed. 40, 42, 43, 44, 46, 46, 46, 48, 50, 51, 51, 59, 67, 67, 69, 70, 79arrow_forwardQuestion 2: A company launches two different marketing campaigns to promote the same product in two different regions. After one month, the company collects the sales data (in units sold) from both regions to compare the effectiveness of the campaigns. The company wants to determine whether there is a significant difference in the mean sales between the two regions. Q: Is there a significant difference in the mean sales between the two regions? Use a 5% significance level. (2 points = 0.25x4 parts) Make null and alternative hypothesis for two sample T-test Conduct Two Sample T test and provide a snapshot of results Null: Alternative: Conclusion: Since the p value is (choose one: less / greater) than 5%,arrow_forward
- Question 3: A marketing agency wants to determine whether different advertising platforms generate significantly different levels of customer engagement. The agency measures the average number of daily clicks on ads for three platforms: Social Media, Search Engines, and Email Campaigns. The agency collects data on daily clicks for each platform over a 10-day period and wants to test whether there is a statistically significant difference in the mean number of daily clicks among these platforms. (2 points = 0.25x4 parts) Make null and alternative hypothesis for ANOVA Conduct ANOVA test and provide a snapshot of results Null: Alternative: Conclusion: Since the p value is (choose one: less / greater) than 5%,arrow_forward8. A large online retailer is analyzing how frequently their product WonderWidget™ is returned. Out of 345 Wonder Widgets bought, 48 were returned. (a) Find the 97% confidence interval for the long-run proportion of WonderWidgets returned. (b) If the retailer wanted to obtain a 97% confidence interval with a margin of error +0.03, how many purchases it should analyze?arrow_forwardBinomial probability problem: A new teaching method claims to improve student engagement. A survey reveals that 60% of students find this method engaging. If 10 students are randomly selected, what is the probability that: a) Exactly 7 students find the method engaging? b) At least 8 students find the method engaging? (please note that “at least 8” is different from 8) Question 1: Binomial probability of exactly 7 students (1 point) Question 2: Binomial probability of at least eight students (1 point)arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning
Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON
The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman
Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman
MATLAB: An Introduction with Applications
Statistics
ISBN:9781119256830
Author:Amos Gilat
Publisher:John Wiley & Sons Inc
Probability and Statistics for Engineering and th...
Statistics
ISBN:9781305251809
Author:Jay L. Devore
Publisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...
Statistics
ISBN:9781305504912
Author:Frederick J Gravetter, Larry B. Wallnau
Publisher:Cengage Learning
Elementary Statistics: Picturing the World (7th E...
Statistics
ISBN:9780134683416
Author:Ron Larson, Betsy Farber
Publisher:PEARSON
The Basic Practice of Statistics
Statistics
ISBN:9781319042578
Author:David S. Moore, William I. Notz, Michael A. Fligner
Publisher:W. H. Freeman
Introduction to the Practice of Statistics
Statistics
ISBN:9781319013387
Author:David S. Moore, George P. McCabe, Bruce A. Craig
Publisher:W. H. Freeman
Statistics 4.1 Point Estimators; Author: Dr. Jack L. Jackson II;https://www.youtube.com/watch?v=2MrI0J8XCEE;License: Standard YouTube License, CC-BY
Statistics 101: Point Estimators; Author: Brandon Foltz;https://www.youtube.com/watch?v=4v41z3HwLaM;License: Standard YouTube License, CC-BY
Central limit theorem; Author: 365 Data Science;https://www.youtube.com/watch?v=b5xQmk9veZ4;License: Standard YouTube License, CC-BY
Point Estimate Definition & Example; Author: Prof. Essa;https://www.youtube.com/watch?v=OTVwtvQmSn0;License: Standard Youtube License
Point Estimation; Author: Vamsidhar Ambatipudi;https://www.youtube.com/watch?v=flqhlM2bZWc;License: Standard Youtube License