
Trigonometry (11th Edition)
11th Edition
ISBN: 9780134217437
Author: Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Question
An airplane is approaching Los Angeles International Airport at an altitude of 10,560 feet. If the horizontal distance from the plane to the runway is 2.1 miles, use the Pythagorean Theorem to find the diagonal distance from the plane to the runway (see the figure below). (5,280 feet equals 1 mile.)
a = 2.1 miles, b = 10,560 feet
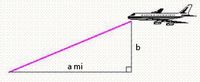
Transcribed Image Text:b.
a mi
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps with 1 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, trigonometry and related others by exploring similar questions and additional content below.Similar questions
- ver. The diagonals of a square:arrow_forwardThe observation deck of the Skylon Tower in Niagra Falls is 166m above the river. Two boats are in the river with passengers looking up at the tower. -Boat A is 60 degrees south of east with an angle of elevation of 50 degrees -Boat B is 130 degrees south of east with an angle of elevation of 56 degrees Calculate the distance between the two boats. Include a diagram for full marks.arrow_forwardA plane starts to take off from the beginning of the runway. When the plane is level with the end of the runway, it is 500 feet above the ground. A bird is flying in the same direction. It is 8 feet above the ground and 15 feet from the begining of the runway. How far is the plane from the beginning of the runway?arrow_forward
- Find the length and midpoint of AB A= -3 B= 21arrow_forwardA forest ranger is 115 feet above the ground in a fire tower when she spots an angry grizzly bear east of the tower with an angle of depression of 10o. Southeast of the tower she spots a hiker with an angle of depression of 15o . Find the distance between the hiker and the angry bear. (Assume that the ground is level; be sure to draw a diagram.)arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Trigonometry (11th Edition)TrigonometryISBN:9780134217437Author:Margaret L. Lial, John Hornsby, David I. Schneider, Callie DanielsPublisher:PEARSON
Trigonometry (11th Edition)TrigonometryISBN:9780134217437Author:Margaret L. Lial, John Hornsby, David I. Schneider, Callie DanielsPublisher:PEARSON Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
 Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning

Trigonometry (11th Edition)
Trigonometry
ISBN:9780134217437
Author:Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher:PEARSON

Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781305652224
Author:Charles P. McKeague, Mark D. Turner
Publisher:Cengage Learning


Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning