
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
please answer with complete method
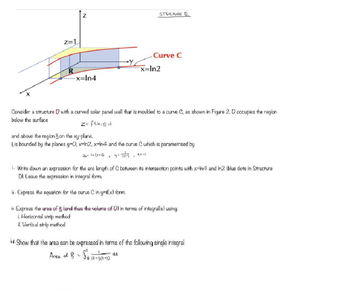
Transcribed Image Text:Z=1
N
-x=In4
Ex
STRUCTURE D
"
Curve C
x=In2
Consider a structure with a curved solar panel wall that is moulded to a curve C, as shown in Figure 2.0 occupies the region
below the surface
z = f(xx,y) =1
and above the region on the xy-plane.
Ris bounded by the planes y=0, x=ln2, x-ln4 and the curve C which is parametrised by
x= In (t+2)
> y = (++)
774
i. Write down an expression for the arc length of C between its intersection points with x-In4 and Im2 (blue dots in Structure
D). Leave the expression in integral form.
ii. Express the equation for the curve C in y=f(x) form.
Express the area of R (and thus the volume of D) in terms of integral(s) using:
i. Horizontal strip method
ii. Vertical strip method
iv. Show that the area can be expressed in terms of the following single integral
Area of B = So (E+1)(4+2)
at
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps with 2 images

Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
where is the solution for question iii
Solution
by Bartleby Expert
Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
where is the solution for question iii
Solution
by Bartleby Expert
Knowledge Booster
Similar questions
- Ve4x-9 xpsarrow_forwardnumber of economy passengers is incorrectarrow_forwardBracket Manufacturing uses a Kanban system for a component. Daily demand is 1,100 units. Each container has a combined waiting and processing time of 0.65 days. If the container size is 100 and the alpha value (a) is 12%, how many Kanban card sets should be authorized? Round your answer up to the whole number. Kanban card set(s) What is the maximum authorized inventory? Use the rounded value from the previous question. Round your answer to the nearest whole number. unit(s)arrow_forward
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

