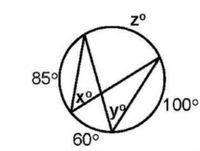
Find the value of X, Y, or Z. ### Understanding Circle Geometry: Angles in a CircleIn this diagram, we observe several angles inside and around a circle, which are crucial in understanding various geometric principles:1. **Angles Inside the Circle**: The diagram features two notable internal angles denoted as \( x^\circ \) and \( y^\circ \).2. **Angles on the Circumference**: An angle marked as \( z^\circ \) is present near the circumference of the circle.3. **External Angles**: Around the circle, three specific angles are identified - \( 85^\circ \), \( 100^\circ \), and \( 60^\circ \).### Analysis of Angles:- The angle \( 85^\circ \) is positioned on the left side, outside the circle.- The angle \( 100^\circ \) is on the right side, also outside the circle.- The angle \( 60^\circ \) is below the circle.These external angles interact with internal angles \( x^\circ \) and \( y^\circ \), providing insight into relationships such as the sum of opposite angles in cyclic quadrilaterals, properties of inscribed angles, and so on.### Key Concepts Illustrated by the Diagram:- **Cyclic Quadrilaterals**: Cyclic quadrilaterals are four-sided figures where each vertex lies on the circumference of a circle. In such quadrilaterals, the sum of each pair of opposite angles is 180°. - **Inscribed Angles**: An inscribed angle in a circle is formed by two chords with a common endpoint. The measure of an inscribed angle is half the measure of its intercepted arc.### Applying the Concepts:By understanding and analyzing such diagrams, students can solve related problems effectively, which further enhances their grasp of fundamental geometric concepts applied frequently in various mathematical contexts.For instance, given the angles around the circle:- The relationship between internal and external angles can be explored.- The values of \( x^\circ \) and \( y^\circ \) can be determined using properties of cyclic quadrilaterals and inscribed angles.This diagram serves as a practical example to visualize and apply the theoretical aspects of circle geometry.

Name: Find the value of X, Y, or Z. ### Understanding Circle Geometry: Angle
Uploaded: 2024-03-20T06:46:14.000Z
Channel: Bartleby
Description: Find the value of X, Y, or Z. ### Understanding Circle Geometry: Angles in a CircleIn this diagram, we observe several angles inside and around a circle, which are crucial in understanding various geometric principles:1. **Angles Inside the Circle**: