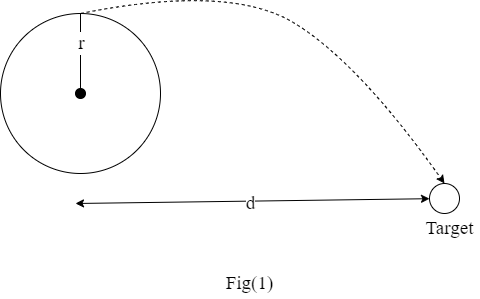
You plan to throw stones by using a sling that you whirl over your head. You will whirl the stone in a horizontal circle with a radius of 1.5 m at a height of 2.9 m above the ground (this is often referred to as a "conical pendulum", which you saw a picture of in the necklace part of the 3-1 studio). You want the stone to hit a target on the ground a distance of 16.5 m in front of you and 1.5 m to the side (note that this number is the same as the radius of the circle). This means that the stone is released a distance 1.5 m to the side of you, but then travels a distance 16.5 m forward. What must be the magnitude of the centripetal acceleration of the stone just before you release it?

When the stone is released it follows a trajectory similar to that of a projectile launched from a height.

Consider the vertical velocity. When the stone is released the horizontal component will not face any resistance but the vertical velocity will be affected by the force of gravity acting on the stone. 

Also, the total vertical distance traveled will be the same as the height from which it was launched.

Thus we can write,

${\mathit{h}}_{\mathbf{y}}\mathbf{=}{\mathit{u}}_{\mathbf{y}}\mathbf{+}\frac{\mathbf{1}}{\mathbf{2}}\mathit{g}{\mathit{t}}^{\mathbf{2}}$

Now initially there will be no vertical velocity, and h_y will be h thus the equation reduces into,

$\begin{array}{rcl}\mathit{h}& \mathbf{=}& \mathbf{0}\mathbf{+}\frac{\mathbf{1}}{\mathbf{2}}\mathit{g}{\mathit{t}}^{\mathbf{2}}\\ \mathit{t}& \mathbf{=}& \sqrt{\frac{\mathbf{2}\mathbf{h}}{\mathbf{g}}}\end{array}$

Also, horizontal velocity will remain constant and can be found out using the equation,

${\mathit{v}}_{\mathbf{x}}\mathbf{=}\frac{\mathbf{d}}{\mathbf{t}}$

Once the velocity is found out we can calculate the acceleration using the formula,

$\mathit{a}\mathbf{=}\frac{{\mathbf{v}}^{\mathbf{2}}}{\mathbf{r}}$