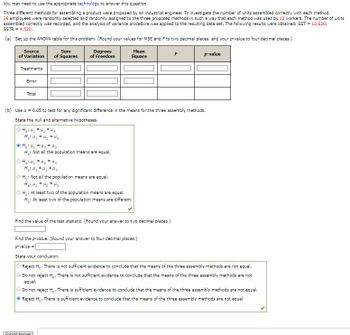
**ANOVA Analysis for Comparing Assembly Methods**To determine if there is a significant difference in the number of units assembled correctly among three different assembly methods, an industrial engineer conducted an experiment with 36 employees. Each method was used by 12 workers, and the number of correctly assembled units was recorded. The analysis of variance (ANOVA) procedure was applied to this data. Below is the detailed transcription and explanation of the analysis:### Data and Instructions for ANOVA Table| **Source of Variation** | **Sum of Squares** | **Degrees of Freedom** | **Mean Square** | **F** | **p-value** ||--------------------------|----------------------|-----------------------------|-----------------|--------|-------------|| Treatments | | | | | || Error | | | | | || Total | | | | | |- SST (Total Sum of Squares) = 12,620- SSTR (Sum of Squares due to Treatments) = 4,520### Steps and Hypotheses**(a) Setup of ANOVA Table**Calculate the degrees of freedom for each source of variation:- **Treatments (Between Groups)**: k - 1 (where k is the number of groups)- **Error (Within Groups)**: N - k (where N is the total number of observations)- **Total**: N - 1 (sum of the two above degrees of freedom)Use the given formulas:- **Mean Square**: MS = SS/df- **F-ratio**: F = MST/MSE **(b) Hypothesis Testing**Using **α = 0.05**, test for a significant difference in means among the three assembly methods.**Hypotheses:**- **Null Hypothesis (H0)**: μ1 = μ2 = μ3 (All means are equal)- **Alternative Hypothesis (Ha)**: Not all means are equalSince the hypotheses are about comparing three methods (μ1, μ2, μ3), the selected hypotheses are:- **H0: μ1 = μ2 = μ3**- **Ha: Not all the population means are equal****Conclusion Derivation**Find the **test statistic** from the ANOVA table and compare it against the F-distribution critical value or directly assess the **p-value** against the significance level (

Anova is a statistical analytical method that used to test the mean of categorical variable with…

You may need to use the appropriate technology to answer this question. Three different methods for assembling a product were proposed by an industrial engineer. To investigate the number of units assembled correctly with each method, 36 employees were randomly selected and randomly assigned to the three proposed methods in such a way that each method was used by 12 workers. The number of units assembled correctly was recorded, and the analysis of variance procedure was applied to the resulting data set. The following results were obtained: SST = 12,620; SSTR = 4,520. (a) Set up the ANOVA table for this problem. (Round your values for MSE and F to two decimal places, and your p-value to four decimal places.) Source Sum Degrees Mean p-value of Variation of Squares of Freedom Square Treatments Error Total (b) Use a = 0.05 to test for any significant difference in the means for the three assembly methods. State the null and alternative hypotheses. OH₂H₂H₂ Hy ⒸHg! H₂H₂H₂ H: Not all the population means are equal. O Hg! H₂H₂H₂ OH,: Not all the population means are equal. H₂H₂H₂H₂ OH: At least two of the population means are equal. H: At least two of the population means are different. Find the value of the test statistic. (Round your answer to two decimal places.) Find the p-value. (Round your answer to four decimal places.) p-value= State your conclusion. O Reject H. There is not sufficient evidence to conclude that the means of the three assembly methods are not equal. O Do not reject H. There is not sufficient evidence to conclude that the means of the three assembly methods are not equal. O Do not reject H. There is sufficient evidence to conclude that the means of the three assembly methods are not equal. Reject H. There is sufficient evidence to conclude that the means of the three assembly methods are not equal.

18th Edition

ISBN:9780079039897

Author:Carter

Publisher:Carter

Chapter10: Statistics

Section: Chapter Questions

Problem 25SGR