MATLAB: An Introduction with Applications
6th Edition
ISBN: 9781119256830
Author: Amos Gilat
Publisher: John Wiley & Sons Inc
expand_more
expand_more
format_list_bulleted
Related questions
Question
The following three independent random samples are obtained from three
H0: µ1 = µ2 = µ3
H1: At least one
a. What is the test statistic that tests the above hypotheses?
b. State the hypotheses for the Bonferroni test between Co-Op and Internship.
H0:
H1:
c. What is the p-value for the Bonferroni test between Co-Op and Internship?
d. Is there a statistically significant difference between the mean starting hourly wage between Co-Op and Internship?
- no
- yes
Transcribed Image Text:← → C
דול ז"
Work Study
Co-Op
Internship
Between Groups
Within Groups
Total
Chapter 11 Homework
Co-Op
Internship
PYANS
19
myopenmath.com/assess2/?cid=166475&aid=12442030#/full
N
15
Dependent Variable: Wage
Bonferroni
24
10
Work Study
DI
Sum of Squares
Mean
47.115
60.300
107.415
12.8767
14.0854
15.6760
(1) Position (J) Position Mean Difference (I-J)
Work Study
Co-Op
Internship
X
df
ANOVA
-1.20875*
-2.79933*
1.20875*
-1.59058*
Internship
Work Study
Co-Op
*. The mean difference is significant at the 0.05 level.
2048
2.79933*
1.59058*
Std. Deviation
Multiple Comparisons
MyOpenMath
2
46
48
52400
1.54058
45556
Mean Square
23.557
Std. Error Sig.
37684 .007
46742 .000
37684 .007
FEB
27
43094 .002
.46742 .000
.43094 .002
1.311
tv
F
95% Confidence Interval
-2.1451
-3.9607
17.971
Lower Bound Upper Bound
2724
-2.6613
1.6379
5198
b Success Con
4.
Sig.
-.2724
-1.6379
2.1451
-.5198
3.9607
2.6613
.000
Mach
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step 1: Given information
VIEW Step 2: a) Obtain the test statistic that test the given hypothesis
VIEW Step 3: b) State the hypotheses for the Bonferroni test between Co-Op and Internship.
VIEW Step 4: c) Obtain the p-value for Bonferroni test between Co-Op and Internship
VIEW Step 5: Conclusion of the Bonferroni test between Co-Op and Internship
VIEW Solution
VIEW 
Step by stepSolved in 6 steps with 13 images
Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
You did not solve part A it is asking for the test statistic not what type of test as you can see above.
Solution
by Bartleby Expert
Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
You did not solve part A it is asking for the test statistic not what type of test as you can see above.
Solution
by Bartleby Expert
Knowledge Booster
Similar questions
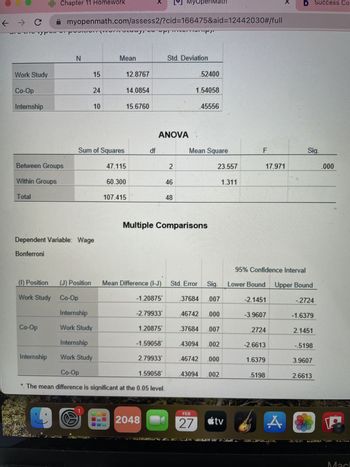
- The following three independent random samples are obtained from three normally distributed populations with equal variances. The dependent variable is starting hourly wage, and the groups are the types of position (work study, co-op, internship). Software was used to conduct a one-way ANOVA to determine if the means are equal using a = 0.10. Summary Statistics: Work Study 12.854 Co-op Internship ANOVA Table: Source Mean Standard Deviation Within Total 14.51 15.424 SS df 132.542 48 0.5487 Work Study vs. Co-op 1.8888 88.0834 46 1.9149 Work Study vs. Internship Co-op vs. Internship 0.449 MS Between 44.4586 2 22.2293 11.6086 8.3E-5 F -3.636 Sample Size Perform a Bonferroni test to see which means are significantly different. Round your answers to three decimal places, and round any interim calculations to four decimal places. Hint: Make sure to use Bonferroni's adjustment. -4.549 15 -1.755 24 10 P-value Test Statistic Adjusted P-value Statistically significant difference? 0.002 0.000…arrow_forwardThe following three independent random samples are obtained from three normally distributed populations with equal variances. The dependent variable is starting hourly wage, and the groups are the types of position (work study, co-op, internship). Software was used to conduct a one-way ANOVA to determine if the means are equal using a = 0.01. Summary Statistics: Work Study 13.1813 Co-op 15.0517 Internship ANOVA Table: Source Between Within Mean Total 15.447 SS 42.1802 Standard Deviation df Work Study vs. Co-op 114.3338 48 Co-op vs. Internship 0.6592 1.6674 72.1536 46 1.5686 Work Study vs. Internship 0.4859 MS F Sample Size 15 24 2 21.0901 13.4452 2.5E-5 10 Perform a Bonferroni test to see which means are significantly different. Round your answers to three decimal places, and round any interim calculations to four decimal places. Test Statistic Adjusted P-value Statistically significant difference? P-value ? ? ?arrow_forwardThe following three independent random samples are obtained from three normally distributed populations with equal variance. The dependent variable is starting hourly wage, and the groups are the types of position (internship, co-op, work study). Group 1: Internship Group 2: Co-op Group 3: Work Study 10.75 12.5 8.5 9.75 10.25 12.5 11.5 13 15.25 10.75 14.25 14.5 11.25 10.5 14 10.5 11 15 13.75 12.75 11.75 11.5 12.5 15.75 11.75 12.75 12 13.25 13.75 14 12.75 14.25 12.25 Conduct a one-factor ANOVA to determine if the group means are equal using α=0.01α=0.01. Group means:Group 1 mean: Group 2 mean: Group 3 mean: ANOVA summary statistics:F-test statistic = p=p= Conclusion: The sample data suggests there is a correlation in the starting hourly wages. There is not sufficient data to conclude that at least one group's average starting hourly wage is different. The sample data suggests the starting hourly wages are dependent There is not…arrow_forward
- The following three independent random samples are obtained from three normally distributed populations with equal variances. The dependent variable is starting hourly wage, and the groups are the types of position (internship, co-op, work study). Round answers to 4 decimal places. Internship Co-op Work Study 13.5 13.5 14.25 14.5 13.25 14.5 14.25 13.5 13.25 13 12.5 13.75 14.75 13 14.5 12.5 12.75 12.75 13.25 13.5 12.5 13.25 14 13.5 13.75 13.5 14 13.25 13 14 13.25 12.5 13.5 13.5 13.5 12.5 13.5 12.75 14.5 14 14.5 14 14.5 14.5 14.25 14.25 13.75 14.75 12.75 12.75 13.25 Use Excel to conduct a single-factor ANOVA to determine if the group means are equal using a = 0.01. Group means: Internship: Со-ор: Work Study: Fill in the summary table for the ANOVA test: df MS Between Within Total From this table, obtain the necessary statistics for the ANOVA: ANOVA summary statistics: Test Statistic = P-value = Conclusion: Select an answerarrow_forwardTwo different types of catalysts are used in a chemical process. We want to conduct a hypothesis test to see if there is a difference in the yields at 5% significance level. Assume both populations are normaly distributed. To this end, we collect a simple random sample from each process. Assume equal variances. = = n-11, n=13,x,-90, x 91.4, 8, 4, 8=4.5arrow_forwardThe following three independent random samples are obtained from three normally distributed populations with equal variances. The dependent variable is movie ticket prices, and the groups are the geographical regions where the theaters are located (suburban, rural, urban). Round answers to at least 4 decimal places. a. Conduct a one-way ANOVA to determine if the group means are equal using alpha=0.01.Group means:Suburb: Rural: Urban: b. ill in the summary table for the ANOVA test: SS df MS Between Within Total c. From this table, obtain the necessary statistics for the ANOVA: ANOVA summary statistics:Test Statistic = p-value =arrow_forward
- The following three independent random samples are obtained from three normally distributed populations with equal variances. The dependent variable is starting hourly wage, and the groups are the types of position (work study, co-op, internship). Software was used to conduct a one-way ANOVA to determine if the means are equal using a = 0.05. Summary Statistics: Work Study 13.1693 Co-op Internship ANOVA Table: Source Mean Standard Deviation Within Total 14.7388 15.441 Between 36.3088 SS df 96.765 48 Work Study vs. Co-op 0.6288 Co-op vs. Internship 1.5401 60.4562 46 1.3143 Work Study vs. Internship 0.2019 MS F Sample Size 15 24 2 18.1544 13.813 2.0E-5 10 Perform a Bonferroni test to see which means are significantly different. Round your answers to three decimal places, and round any interim calculations to four decimal places. Test Statistic Adjusted P-value Statistically significant difference? P-value ? ? ?arrow_forwardHere is a link to a data set concerning treatment groups A and B. Before performing a t-test to determine if the two groups are different, researchers must first ascertain if the variance in the two groups is the same using an F test. Indicate whether the hypothesis below is the null or alternate hypothesis for the F test. The variance in group A is equal to the variance in group B Calculate the F statistic for this data set and report it in the box below, rounded to two decimal places. Use the formula =(1-(f.dist(F, df1,df2,true) in Excel to calculate the P value for the F statistic, and report it in the box below. Do not use the rounded value for F when calculating the P value. Use the value in the spreadsheet that has not been rounded. Based on this p value, would you recommend using a Student's t test or a Welch's t test to determine if the two treatment groups have different means? Enter either Student's or Welch's in the box below.arrow_forwardThe following three independent random samples are obtained from three normally distributed populations with equal variances. The dependent variable is starting hourly wage, and the groups are the types of position (internship, co-op, work study). Round answers to 4 decimal places. Internship Со-ор Work Study 15 14.5 15.25 13.75 13.5 16.5 15.5 12 12.75 13 15.75 14.75 14.5 15.25 13.5 13 12.25 15.25 16.75 13.75 13.25 17.25 13 15 13.5 12.5 14.75 13.5 12.25 13.25 14.25 13 16.5 14.75 16 16 14.5 12.75 15 15.5 16.75 14.75 16.25 14 14.25 Use Excel to conduct a single-factor ANOVA to determine if the group means are equal using a = 0.02. %3D Group means: Internship: Со-ор: Work Study: Fill in the summary table for the ANOVA test: df MS Between Within Total From this table, obtain the necessary statistics for the ANOVA: ANOVA summary statistics: Test Statistic = p-value = Conclusion: Select an answerarrow_forward
- In an industrial experiment, a job was performed by 10 workers using Method I, and by 7 workers using Method II. The experiment yielded the following data. The unit of measurement is minute. A statistician wants to test for the equality of two variances and the difference in the mean times to complete the job using the two methods. (This is a case of two independent samples drawn from two normal populations). Method 1 Method 2 12221915101615222613 61071261012 n1=10 Mean=17 Variance=26 n2=7 Mean=9 Variance=7 (a) Test at the 5% significance level whether the two variances are equal. (Give null and the alternative hypotheses, test statistic, rejection rule, conclusion) (b) Estimate with 95% confidence the ratio of the two population variances. Briefly describe what the interval estimate tells you. (c) Briefly explain how to use the interval estimate in part (b) to test the hypotheses in (a).arrow_forwardTwo separate samples, each with 16 individuals, receive two different treatments. After treatment, the first sample has SS = 1540 and the second has SS = 1460. a. Find the pooled variance, s2p, for the two samples b. The estimated standard error is c. If the sample mean difference is 10 points (i.e., M1 - M2 = 10), compute the t-statistic. The t-statistic is:arrow_forwardThe following three independent random samples are obtained from three normally distributed populations with equal variance. The dependent variable is starting hourly wage, and the groups are the types of position (internship, co-op, work study). Group 2: Co-op Group 3: Work Study Group 1: Internship 10 10.5 11.25 11 9.25 10.25 9.75 13.25 10.5 12.5 10.5 10.75 Use technology to conduct a one-factor ANOVA to determine if the group means are equal using a = 0.01. Group means (report to 2 decimal places): Group 1: Internship: Group 2: Co-op: Group 3: Work Study: ANOVA summary statistics: F-ratio = (report accurate to 3 decimal places) 12.25 10.5 10.75 11.5 10 10.5 р (report accurate to 4 decimal places) Conclusion: © The sample data suggest the average starting hourly wages are not the same. O There is not sufficient data to conclude the starting wages are different for the different groups.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
- MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning 
Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON
The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman
Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman
MATLAB: An Introduction with Applications
Statistics
ISBN:9781119256830
Author:Amos Gilat
Publisher:John Wiley & Sons Inc
Probability and Statistics for Engineering and th...
Statistics
ISBN:9781305251809
Author:Jay L. Devore
Publisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...
Statistics
ISBN:9781305504912
Author:Frederick J Gravetter, Larry B. Wallnau
Publisher:Cengage Learning
Elementary Statistics: Picturing the World (7th E...
Statistics
ISBN:9780134683416
Author:Ron Larson, Betsy Farber
Publisher:PEARSON
The Basic Practice of Statistics
Statistics
ISBN:9781319042578
Author:David S. Moore, William I. Notz, Michael A. Fligner
Publisher:W. H. Freeman
Introduction to the Practice of Statistics
Statistics
ISBN:9781319013387
Author:David S. Moore, George P. McCabe, Bruce A. Craig
Publisher:W. H. Freeman