Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Related questions
Question
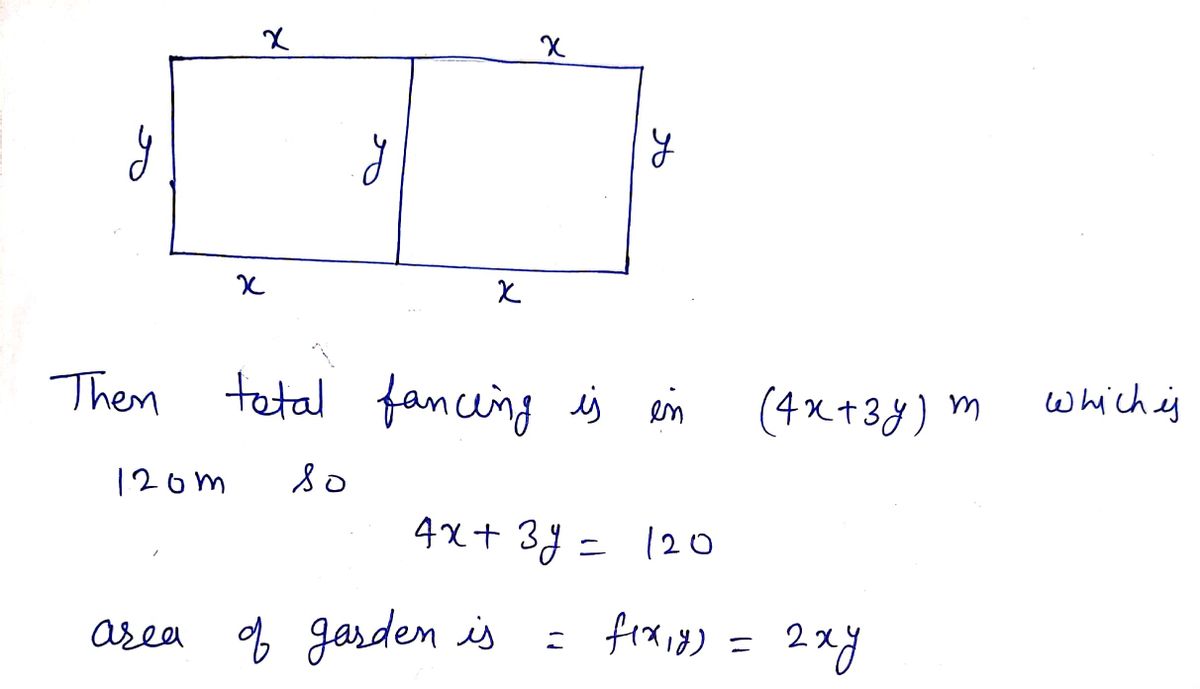
![**Title: Maximizing Area with Limited Fencing**
**Problem Description:**
You are tasked with fencing off two rectangular garden beds of the same size such that they share one side. Given that you have 120 meters of fencing, what is the maximum total area (in square meters) that you can fence off in this way?
**Diagram Explanation:**
The diagram shows two rectangles laid out side by side, sharing a common side. The length of the shared side is denoted as \( x \), and the width of each rectangle is denoted as \( y \).
The fencing requirements include:
- Two widths (\( 2y \))
- Two lengths (\( x \))
- One additional dividing length (\( x \))
The total length of the fencing used is given by the formula:
\[ 3x + 2y = 120 \]
The total area \( A \) of the two rectangles, which needs to be maximized, can be expressed as:
\[ A = 2xy \]
**Objective:**
Find the optimal values for \( x \) and \( y \) that maximize the total area \( A \) under the constraint of the available fencing.](https://content.bartleby.com/qna-images/question/d94ee947-1f00-4d5c-8d00-18458a43a16b/144f5d5c-9447-46c0-a2e1-0e587e7cf92e/0frck3m_processed.jpeg)
Transcribed Image Text:**Title: Maximizing Area with Limited Fencing**
**Problem Description:**
You are tasked with fencing off two rectangular garden beds of the same size such that they share one side. Given that you have 120 meters of fencing, what is the maximum total area (in square meters) that you can fence off in this way?
**Diagram Explanation:**
The diagram shows two rectangles laid out side by side, sharing a common side. The length of the shared side is denoted as \( x \), and the width of each rectangle is denoted as \( y \).
The fencing requirements include:
- Two widths (\( 2y \))
- Two lengths (\( x \))
- One additional dividing length (\( x \))
The total length of the fencing used is given by the formula:
\[ 3x + 2y = 120 \]
The total area \( A \) of the two rectangles, which needs to be maximized, can be expressed as:
\[ A = 2xy \]
**Objective:**
Find the optimal values for \( x \) and \( y \) that maximize the total area \( A \) under the constraint of the available fencing.
Expert Solution
arrow_forward
Step 1
Step by stepSolved in 2 steps with 2 images
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Similar questions
- A rectangular zone measuring 12 miles by 16 miles contains five buildings. What is the maximum distance separating each building from the others? (Input your answer as a number without units.)arrow_forwardYou are to fence off two rectangular garden beds of the same size in such a way that they share one side. Given that you have 120m of fence, what is the maximum total area (in m2) that you can fence off in this way? yarrow_forwardA framer has 160 feet of fencing to enclose two adjacent rectangular pens. what dimensions should he use for the length and width of each pen so that total area enclosed is a maximum?arrow_forward
Recommended textbooks for you
- Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY 
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education
Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,