You are managing an investment portfolio and sell an “inflation-protected” annuity that pays $3,862 per month (in real terms) for 7 years, starting next month. You forecast that inflation will be 0.45% per month over the 7 years. If you earn 4.17% APR (monthly compounding) nominal terms on your investments, how much do you need to invest today to fully fund the annuity?
You are managing an investment portfolio and sell an “inflation-protected”
If you earn 4.17% APR (monthly compounding) nominal terms on your investments, how much do you need to invest today to fully fund the annuity?
The present value is the value of the sum received at time 0 or the current period. It is the value of the sum that will be received in the future period.
The annual payment of annuity is $3,862 per month. The time period is 7 years and the annual percentage rate is 4.17%. The inflation rate is 0.45% per month.
Compute the monthly interest rate, using the equation as shown below:
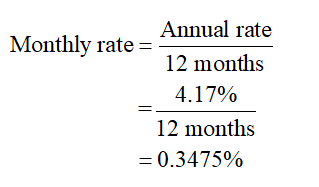
Hence, the monthly interest rate is 0.3475%.
Compute the present value annuity factor (PVIFA), using the equation as shown below:
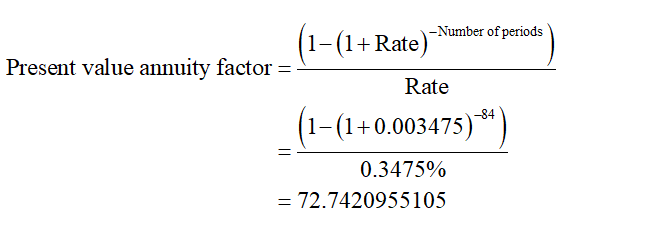
Hence, the present value annuity factor is 72.7420955105.
Step by step
Solved in 5 steps with 3 images
