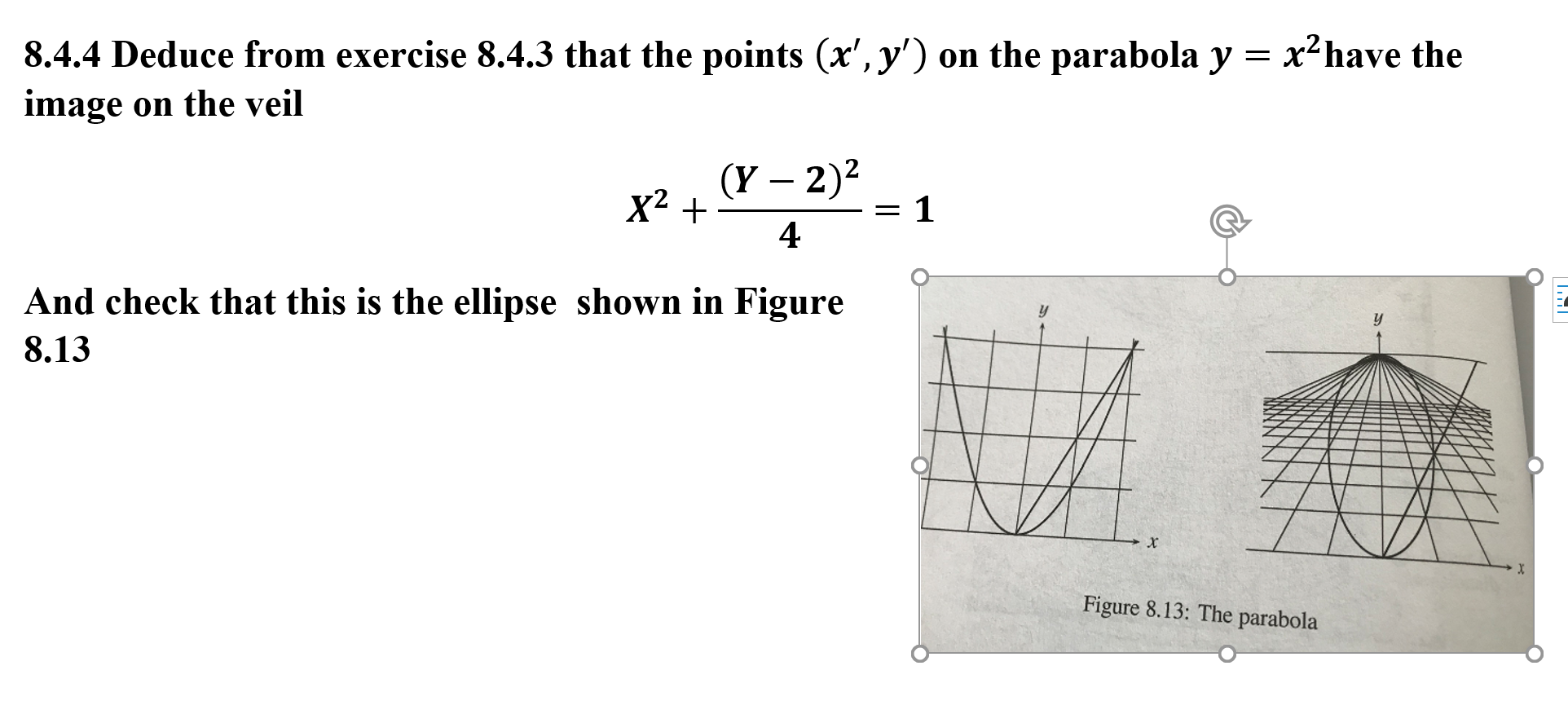
x2have the 8.4.4 Deduce from exercise 8.4.3 that the points (x', y') on the parabola y image on the veil (Y 2)2 X2 1 4 And check that this is the ellipse shown in Figure 8.13 x Figure 8.13: The parabola S-8.4.2-8.4.4,8.7.1,8.7.2,9.2.2,9.2.5,9.5.1,9.5.2 8.4.3 Renaming the coordinates x,z in the veil as X,Y respectively show that 8.4.2 Find the parametric equations of the line from (0, -4,4) to (x',y',0) and hence show 4X 4Y у 4 Y that this line meets the veil where: 4- Y' 4x' 4y' Solve for y as follows: X = Z = y'4 y4 4y Y(y' 4) 4y Y = y' 4 х — х' у — у' z-0 х' — 0 y' 4 0 4 4y' 4Y = 4y' - y'Y y'Y4Y х — х' У — у" Z 4Y y'(4- Y) (1) y' 4 у — у" х' -4 4Y y= 4 Y х — х' х' y' 4 Solve for x as follows: — х(у' + 4) — х'(у' + 4) — х'(у — у') 4c and obtain the equation for x' below: y'+4 Substitute the equation obtained for y' in x = — х(у' + 4) — х'(у' + 4 + у-у) — 0 — х(у' + 4) — х'(4 + у) 4x' 4Y = 4x + - 4Y x'(4y (y' + 4) +4 (2) X = 4XY 4X = 4x'> 4XY + 4X(4 — Ү) = 4x У — у" y' 4 Z 4 Y 4 Y -4 XҮ + X(4 — Ү) = x' 4 Y XҮ + 4X — XҮ = x — 2(y' + 4) — -4(у — у') 4 Y 4(y' — у) 4X x' = Z 4 Y y'4 The line (1) meets the veil at y = 0 hence (2) (3) 4X 4Y Hence it is proved that x' = y 4-ү' 4x — х %— 4y' ; У 4-Yг %3D 0 : Z= y'4 y'4 х-х' Suppose у-у' y'+4 = k -4 x' х 3 (k+ 1)x' y - y' ky 4) y k(y' + 4) + y' z -4k Also suppose у' у'+4 х1 4(1 a) х — ах',z 3 аy',4 — аy' + 4а — у' — ; z = 4(1 - a) a Hence parametric equation is given by: x (k 1)x'; y = (k + 1)y'+ 4k; z = -4k