
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
5.2) Solve the given system of equations using Gauss-Jordan Reduction method
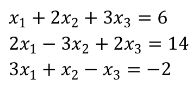
Transcribed Image Text:x1 + 2x2 + 3x3 = 6
2х1 - 3х2 + 2x3 = 14
3x1 +x2-x3 =-2
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 3 steps with 4 images

Knowledge Booster
Similar questions
- 1. (a) Use definition of linear transformation to determine whether the transformation T:R? → R³ defined as follows is linear. -y T r+ 2y 2.r – 4y (b) Let T : R" → R" be a linear transformation. i. Is it always true that T(0) = 0 where the zero vectors live in the appropriate spaces? Justify. ii. Does S(0) = 0 mean that S is linear? If not, can you give a counter-example? (c) Consider the following matrix transformation T : R² → R² defined as a b T d i. If T rotates the 2D space 150° counter-clockwise, and then reflects the result across the new r-axis, find a, b, c, d. ii. What if T reflects the 2D space across the r-axis first and then rotates 150° counter-clockwise? Do you expect to get the same a, b, c, d? Why or why not?arrow_forwardQ1) Solve the following linear system of equations using Gauss elimination and using Cramer's rule. (2 + 3i)x + (2 – i)y = (1 +2i) (4 + 2i)x + (2 + i)y = 2 а) %3| b) (2+ )х + (1 — i)у %3D 2 4ix + (2 + 4i)y = i Q2 Find all solution for cos(z) = 10arrow_forward1) Utilize the fourth order Taylor polynomial for e7x at x=0 in order to approximate the value of e1.2 2) Utilize the Taylor series remainder estimate in order to bound the error in the approximation in #1, where the absolute value of the difference between the actual value and the approximation that's been made:arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

