
Elementary Geometry For College Students, 7e
7th Edition
ISBN: 9781337614085
Author: Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher: Cengage,
expand_more
expand_more
format_list_bulleted
Question
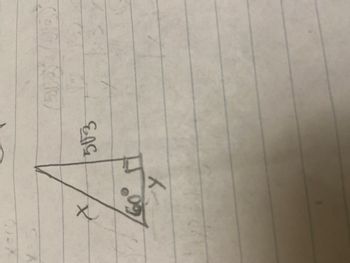
Transcribed Image Text:### Educational Content on Right Triangles
**Right Triangle with Given Measures**
In this figure, we have a right triangle characterized by:
- One angle measuring \(60^\circ\)
- A right angle (\(90^\circ\))
- One side labeled as \(x\)
- Another side labeled as \(y\)
- The hypotenuse labeled as \(50\sqrt{3}\)
This right triangle is a special type of triangle known as a 30°-60°-90° triangle, which has specific relationships between the lengths of its sides. The sides of a 30°-60°-90° triangle follow these ratios:
- The side opposite the 30° angle (the shortest side) is half the length of the hypotenuse.
- The side opposite the 60° angle (the longer leg) is \( \sqrt{3} \) times the length of the side opposite the 30° angle.
For this specific triangle:
- Given that the hypotenuse is \(50\sqrt{3}\), the side opposite the 30° angle (y) is half of the hypotenuse. Therefore, \( y = \frac{50\sqrt{3}}{2} = 25\sqrt{3} \).
- The side opposite the 60° angle (x) is \( \sqrt{3} \) times the side opposite the 30° angle. Therefore, \( x = 25\sqrt{3} \cdot \sqrt{3} = 25 \cdot 3 = 75 \).
### Key Takeaways
- **Angle Measures**: The triangle includes angles of 30°, 60°, and 90°.
- **Side Ratios**: For a 30°-60°-90° triangle, the ratios between the sides are consistent and allow for easy calculation of unknown sides if at least one side length is known.
By understanding these properties, solving for the unknown side lengths in similarly-structured right triangles becomes straightforward.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps

Knowledge Booster
Similar questions
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning

Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,

Elementary Geometry for College Students
Geometry
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Cengage Learning