
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
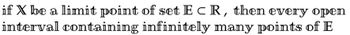
Transcribed Image Text:if X be a limit point of set ECR, then every open
interval containing infinitely many points of E
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Similar questions
- 2. Prove tne Follow Statements: (i) The infimum of a set S ip it exist ,lt is unique. 11) Let AC IK be a non-empty Subset of positive real numbers which is bounded above and let r70. Detine the following Subset of IR. B = Cr+a: aCAY and C=[ra : a6 AJ Prove that If Sup(A)=u, then Sup(B) =rtu and Sup (c) =ru.arrow_forwardUsing the set definition, prove for any set X, Y and Z applyarrow_forward8 /9 75% Prove that if A, B.C are subsets of a universal set U, then AU(BnC) C (AUB)n(AUC). ere to search D altarrow_forward
- Let A, B, C be arbitrary finite sets from the same universal set U. - - (a) Is it true that A - B C (A - B) – (B − C)? If "yes", then prove "rigorously"; if "no", then show a concrete counterexample by specifying sets A, B, C where this subset relation does not hold. (To prove an expression of the form MCN "rigorously", you need to consider an arbitrary element x from M and show that x E N.) (b) Is it true that (A - B = A - C) → (B = C)? If "yes", then prove "rigorously"; if "no", then show a concrete counterexample by specifying sets A, B, C where this implication does not hold.arrow_forwardProvide Cantor’s proof that the set (0, 1) is uncountable.arrow_forward1. Find the supremum, infimum, maximum, and minimum of each subset of R, if it exists. a. A = sup A max A inf A U[-1-] TEN min A = {":neN} b. B = sup B max B inf B min B c. C = {re Q:r² ≥ 1} sup C max C inf C min C Q Search DOLL 1arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

