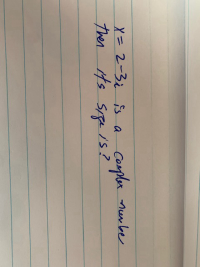
see attached ### Understanding the Form of a Complex NumberConsider the complex number expressed as \( Y = 2 - 3i \). In this expression:- **2** is the **real part** of the complex number.- **-3i** is the **imaginary part** of the complex number, where \( i \) is the imaginary unit, representing the square root of -1.#### Identifying Components:- **Real Part**: The coefficient of the number without the imaginary unit \( i \). For \( Y = 2 - 3i \), the real part is **2**.- **Imaginary Part**: The coefficient of the imaginary unit \( i \). For \( Y = 2 - 3i \), the imaginary part is **-3**.If asked, "What is its sign?" the context is typically about the imaginary part unless otherwise specified. Here, the imaginary part is -3.### SummaryGiven a complex number \( Y = 2 - 3i \):- The **real part** is **2**.- The **imaginary part** is **-3**.Understanding these components is crucial in performing operations with complex numbers, such as addition, subtraction, and multiplication.

Name: see attached ### Understanding the Form of a Complex NumberConsider th
Uploaded: 2024-03-20T06:46:14.000Z
Channel: Bartleby
Description: see attached ### Understanding the Form of a Complex NumberConsider the complex number expressed as \( Y = 2 - 3i \). In this expression:- **2** is the **real part** of the complex number.- **-3i** is the **imaginary part** of the complex number, whe