Write a regular expression to describe each of the following languages. Example: {w € [a, b}* : w has both aa and bb as substrings} Regular expression: (a U b)* aa (a U b)* bb (a U b)* U (a U b)* bb (a U b)* aa (a U b)*
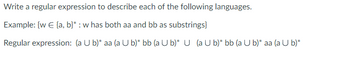
![(3) {w € [0, 1]*: w corresponds to the binary encoding, without leading O's, of natural numbers that
are powers of 4}
1(00)*
O (10)*0
O (10)*1
O 1(01)*](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F6b67a6a2-2d8c-4553-99c2-3c44a5ebdd4f%2F0528d3ef-29fa-4cab-8956-1f109c0618b3%2F9cjxser_processed.png&w=3840&q=75)
(a) In regular expression theory, a regular expression is a pattern that defines a set of strings over an alphabet. Regular expressions are commonly used in computer science and programming to perform various operations such as searching, matching, and parsing text data. In this question, we are asked to construct a regular expression for the language of binary strings that do not begin with an "a".
Before we dive into constructing the regular expression, let's first clarify some basic concepts. In a binary alphabet, we have two symbols: 0 and 1. A binary string is a sequence of 0's and 1's. The length of a binary string is the number of symbols in the string. For example, "11001" is a binary string of length 5. A language over a binary alphabet is a set of binary strings. For example, the language of all binary strings of length 3 is {000, 001, 010, 011, 100, 101, 110, 111}.
Now, let's focus on the language of binary strings that do not begin with an "a". To construct a regular expression for this language, we need to define a pattern that matches any binary string that does not start with "a". In a binary alphabet, "a" is not a valid symbol, so we need to find a way to express this concept using the symbols that we have. One way to do this is to say that any binary string that does not start with "a" must start with either "0" or "1". We can express this using the following regular expression:
(0|1)*
This regular expression matches any number (including zero) of "0"s or "1"s. However, this regular expression also matches binary strings that start with "a". To exclude those strings, we need to add a condition that ensures the first symbol is not "a". We can express this condition by requiring that the first symbol is "1". We can modify the previous regular expression to achieve this:
1(0|1)*
This regular expression matches any binary string that starts with "1" and is followed by any number (including zero) of "0"s or "1"s. Since "a" is not a valid symbol in a binary alphabet, this regular expression matches any binary string that does not begin with "a".
To break this regular expression down further, we can start by looking at the first symbol, which is "1". This symbol matches only itself. The parentheses around the (0|1)* portion of the regular expression indicate that the enclosed expression can be repeated any number of times (including zero). The (0|1)* portion matches any number of "0"s or "1"s after the first "1". Together, this regular expression matches any binary string that starts with "1" and is followed by any number (including zero) of "0"s or "1"s, which is the language of binary strings that do not begin with an "a".
In conclusion, the regular expression for the language of binary strings that do not begin with an "a" is:
1(0|1)*
This regular expression matches any binary string that starts with "1" and is followed by any number (including zero) of "0"s or "1"s. It excludes binary strings that start with "a", which is not a valid symbol in a binary alphabet.
Step by step
Solved in 4 steps
