
MATLAB: An Introduction with Applications
6th Edition
ISBN: 9781119256830
Author: Amos Gilat
Publisher: John Wiley & Sons Inc
expand_more
expand_more
format_list_bulleted
Topic Video
Question
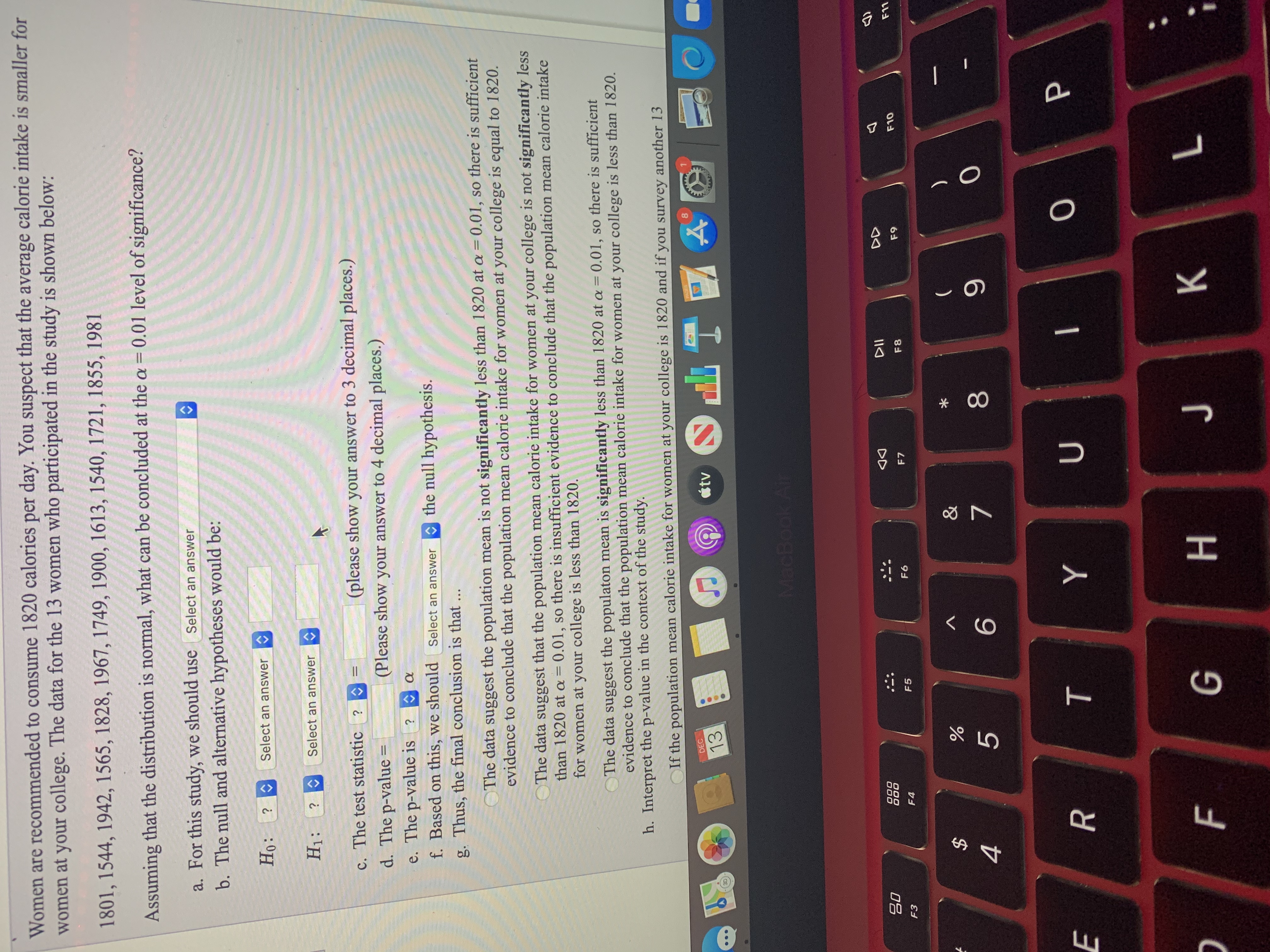
Women are recommended to consume 1820 calories per day. You suspect that the average calorie intake is smaller for women at your college. The data for the 13 women who participated in the study is shown below:
1801, 1544, 1942, 1565, 1828, 1967, 1749, 1900, 1613, 1540, 1721, 1855, 1981
Assuming that the distribution is normal, what can be concluded at the αα = 0.01 level of significance?
- For this study, we should use Select an answer t-test for a population
mean z-test for a population proportion - The null and alternative hypotheses would be:
H0:H0: ? μ p Select an answer ≠ = < >
H1:H1: ? p μ Select an answer ≠ = < >
- The test statistic ? t z = (please show your answer to 3 decimal places.)
- The p-value = (Please show your answer to 4 decimal places.)
- The p-value is ? ≤ > αα
- Based on this, we should Select an answer fail to reject accept reject the null hypothesis.
- Thus, the final conclusion is that ...
- The data suggest the population mean is not significantly less than 1820 at αα = 0.01, so there is sufficient evidence to conclude that the population mean calorie intake for women at your college is equal to 1820.
- The data suggest that the population mean calorie intake for women at your college is not significantly less than 1820 at αα = 0.01, so there is insufficient evidence to conclude that the population mean calorie intake for women at your college is less than 1820.
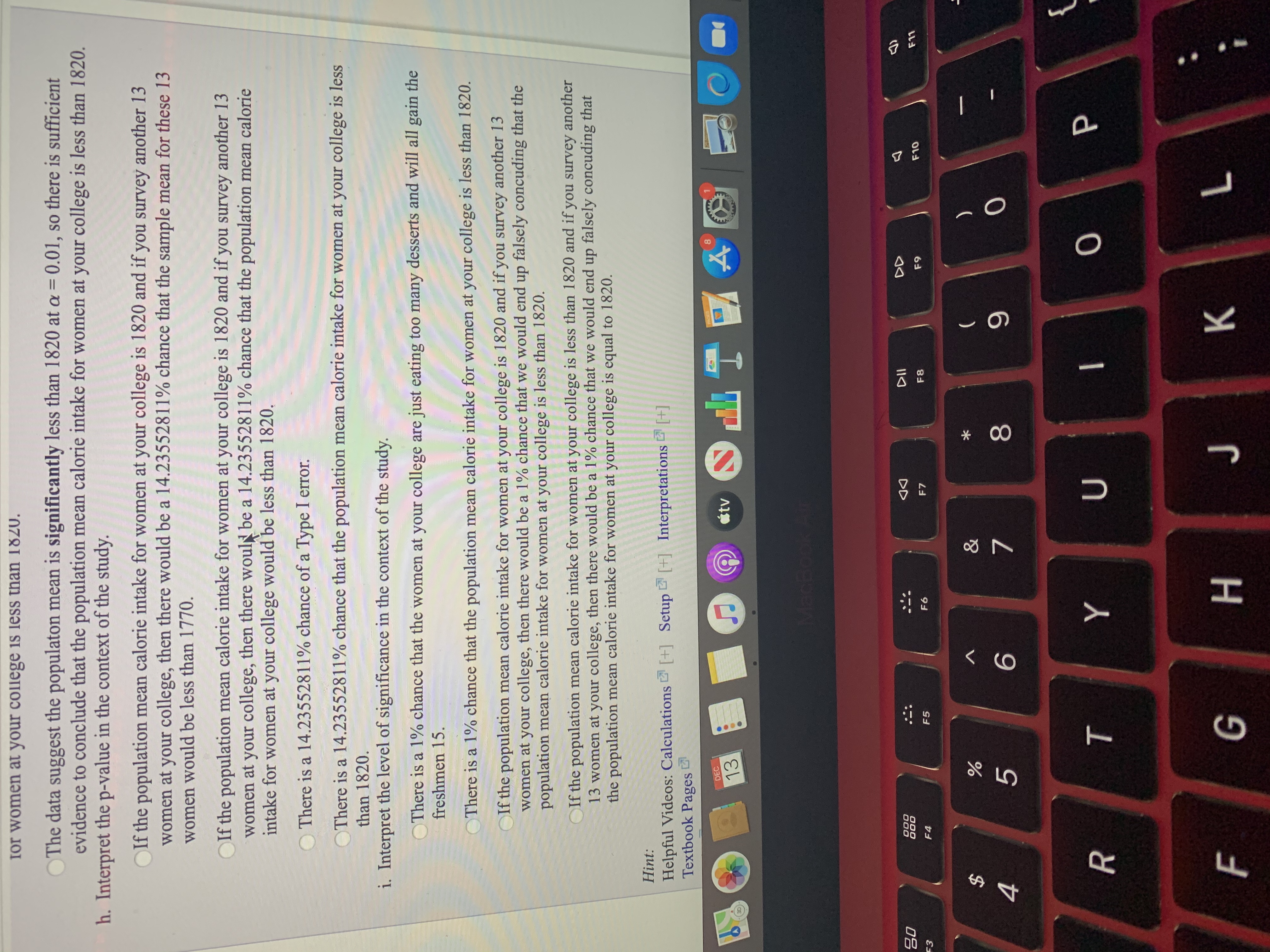
- The data suggest the populaton mean is significantly less than 1820 at αα = 0.01, so there is sufficient evidence to conclude that the population mean calorie intake for women at your college is less than 1820.
- Interpret the p-value in the context of the study.
- If the population mean calorie intake for women at your college is 1820 and if you survey another 13 women at your college, then there would be a 14.23552811% chance that the sample mean for these 13 women would be less than 1770.
- If the population mean calorie intake for women at your college is 1820 and if you survey another 13 women at your college, then there would be a 14.23552811% chance that the population mean calorie intake for women at your college would be less than 1820.
- There is a 14.23552811% chance of a Type I error.
- There is a 14.23552811% chance that the population mean calorie intake for women at your college is less than 1820.
- Interpret the level of significance in the context of the study.
- There is a 1% chance that the women at your college are just eating too many desserts and will all gain the freshmen 15.
- There is a 1% chance that the population mean calorie intake for women at your college is less than 1820.
- If the population mean calorie intake for women at your college is 1820 and if you survey another 13 women at your college, then there would be a 1% chance that we would end up falsely concuding that the population mean calorie intake for women at your college is less than 1820.
- If the population mean calorie intake for women at your college is less than 1820 and if you survey another 13 women at your college, then there would be a 1% chance that we would end up falsely concuding that the population mean calorie intake for women at your college is equal to 1820.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 3 steps with 1 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, statistics and related others by exploring similar questions and additional content below.Similar questions
- Three sample observations taken for two variables are shown below: X (In $) (In ounces) 2.78 0.60 1.79 1.47 0.80 2.34 When comparing X and Y, which varies the most? What is the value of this statistic (ornitting unit labels such as $, s2, ounces, ounces Ca. Y, 59.1837 Ob. X, 61.7026 CC. Y, 0.8700 Od. None of the answers is correct Ce. X, 0.9801arrow_forwardWomen are recommended to consume 1720 calories per day. You suspect that the average calorie intake is different for women at your college. The data for the 12 women who participated in the study is shown below: 1837, 1618, 1820, 1846, 1640, 1700, 1655, 1473, 1563, 1840, 1796, 1854 Assuming that the distribution is normal, what can be concluded at the αα = 0.10 level of significance? For this study, we should use Select an answer z-test for a population proportion t-test for a population mean The null and alternative hypotheses would be: H0:H0: ? μ p Select an answer > < ≠ = H1:H1: ? p μ Select an answer ≠ = < > The test statistic ? t z = (please show your answer to 3 decimal places.) The p-value = (Please show your answer to 4 decimal places.) The p-value is ? > ≤ αα Based on this, we should Select an answer reject accept fail to reject the null hypothesis. Thus, the final conclusion is that ... The data suggest that the population mean…arrow_forwardWomen are recommended to consume 1700 calories per day. You suspect that the average calorie intake is different for women at your college. The data for the 12 women who participated in the study is shown below: 1784, 1677, 1583, 1984, 1910, 1737, 1522, 1574, 1853, 1546, 1707, 1866 Assuming that the distribution is normal, what can be concluded at the αα = 0.10 level of significance? For this study, we should use The null and alternative hypotheses would be: H0:H0: H1:H1: The test statistic = (please show your answer to 3 decimal places.)arrow_forward
- Please help me with the following sections: d, e, f, g, h and i Thank you!arrow_forward. Do patients with gastrointestinal issues experience more psychological distress than the general population? The DASS-21 questionnaire is a validated measure of depression, anxiety, and stress. For the general population, the mean for anxiety is µ = 4.2. Anxiety levels are calculated based on self-reported answers to questions on a scale from 0 through 42, with lower scores indicating lower anxiety. Participants with gastrointestinal issues (specifically inflammatory bowel disease, IBD) completed the DASS-21. Use the data presented below to determine whether having gastrointestinal issues like IBD significantly increases risk for anxiety. Test whether or not the performance of this sample is significantly higher than the normal population using the proper t-test. Here are the data: Anxiety scores: 12, 15, 10, 8, 10, 5, 10, 13, 4, 6 ANALYSES AND UNGRADED OPTIONAL GUIDING QUESTIONS: 1a. Identify the Indep.Variable:__ Dep.Variable:__ Is it the Hypothesis…arrow_forwardOn occasion, medical studies need to model the proportion of the population that has a disease and compare that to observed frequencies of the disease actually occurring. Suppose the end-stage renal failure in south-west Wales was collected for different age groups. Do the data in the table show that the observed frequencies are in agreement with proportion of people in each age group? Test at the 1% level. Renal Failure Frequencies Age group 16-29 30-44 45-59 60-74 75+ Total Observed Frequencies 125 152 134 124 48 583 Expected Proportion 0.23 0.25 0.22 0.21 0.09 State the hypotheses.H0: The observed frequencies in agreement with proportion of people in each age group.Ha: The observed frequencies in agreement with proportion of people in each age group. Calculate the χ2 test statistic. Round expected values to two decimal places. Round χ2 to 3 decimal places.χ2 = Calculate the p-value. Round to 3 decimal places.p-value = State your decision.Since p-value α,…arrow_forward
- Historically, Olympic officials have reported testosterone levels in general should be u = 538 ng/dL, with o = 189, with x being normally distributed. Summer Olympic sprinters (n = 8) from the U.S. were tested for testosterone levels the morning after the opening ceremonies. Their sample mean was ng/dL. Do these data indicate that the sprinters had an overall average testosterone level greater than 538? Use a = .05. State a, H,, H1, p-value, rejection, or non-rejection, and be certain to interpret your results.arrow_forwardOst watched Ani... Question 2 Y Part 1 of 4 A doctor in Cleveland wants to know whether the average life span for heart disease patients at four hospitals in the city differ. The data below represents the life span, in years, of heart disease patients from each hospital. Perform an ANOVA test with a 9% level of significance to test whether the average life span of heart disease patients in Cleveland differs depending on the hospital that treats them Life Span of Patients Treated at Hospital 1: 7.4, 7.8, 7.7, 7.5, 8, 8.2, 7.8, 8.6, 8, 7.8, 8.3, 8.3, 8, 7.6, 8.2, 7.9, 7.3, 8, 8.6, 7.3, 8.3, 8, 7.8, 8, 7.8, 8.1, 8.1, 8, 7.6, 7.6, 7.7, 7.4, 7.7, 7.8, 7.8 Life Span of Patients Treated at Hospital 2: 7.9, 7.9, 8.2, 8, 8.1, 8.5, 8.3, 8.4, 8, 8.2, 7.7, 8, 8, 7.8, 7.9, 8.1, 8.1, 7.8, 7.9, 8, 8.5, 8.3, 8.2, 8.3, 7.8, 7.9 Life Span of Patients Treated at Hospital 3: 8.2, 8.1, 7.4, 8.7, 8.6, 8.2, 7.9, 8.1, 8.1, 8.3, 8.3, 8, 7.6, 8, 7.4, 8.6, 8.2, 8.2, 7.9, 7.7, 8.1, 7.9, 8, 8.3 Life Span of…arrow_forwardWomen are recommended to consume 1700 calories per day. You suspect that the average calorie intake is different for women at your college. The data for the 12 women who participated in the study is shown below: 1808, 1681, 1723, 1847, 1808, 1858, 1461, 1449, 1631, 1635, 1815, 1874 Assuming that the distribution is normal, what can be concluded at the αα = 0.01 level of significance? For this study, we should use The null and alternative hypotheses would be: H0:H0: H1:H1: The test statistic = (please show your answer to 3 decimal places.) The p-value = (Please show your answer to 4 decimal places.) The p-value is αα Based on this, we should the null hypothesis. Thus, the final conclusion is that ... The data suggest the population mean is not significantly different from 1700 at αα = 0.01, so there is sufficient evidence to conclude that the population mean calorie intake for women at your college is equal to 1700. The data…arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning
Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON
Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman
The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman
Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman

MATLAB: An Introduction with Applications
Statistics
ISBN:9781119256830
Author:Amos Gilat
Publisher:John Wiley & Sons Inc

Probability and Statistics for Engineering and th...
Statistics
ISBN:9781305251809
Author:Jay L. Devore
Publisher:Cengage Learning

Statistics for The Behavioral Sciences (MindTap C...
Statistics
ISBN:9781305504912
Author:Frederick J Gravetter, Larry B. Wallnau
Publisher:Cengage Learning

Elementary Statistics: Picturing the World (7th E...
Statistics
ISBN:9780134683416
Author:Ron Larson, Betsy Farber
Publisher:PEARSON

The Basic Practice of Statistics
Statistics
ISBN:9781319042578
Author:David S. Moore, William I. Notz, Michael A. Fligner
Publisher:W. H. Freeman

Introduction to the Practice of Statistics
Statistics
ISBN:9781319013387
Author:David S. Moore, George P. McCabe, Bruce A. Craig
Publisher:W. H. Freeman