
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
thumb_up100%
Number 1 and 2. SOLVE for Lm, Pm, and Wm. I attached a reference for the solving method.
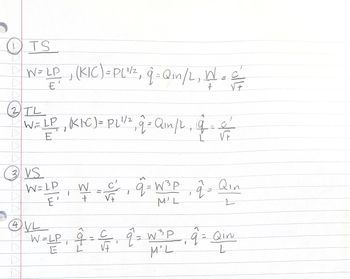
Transcribed Image Text:Po
TS
| W=LP₁ (KIC) =PL¹/₂²₁ 9 = Qin/2, N =
E'
c
7
+
IL
-
W = LP₁ (KIC) = PL¹/²₂ 9 = Q₁n/2, 19
L
E
ان
VF
3VS
1
c'
W=LD W €²₁ 9=W³P 2 - Qin
q=
1
1
q
E'
+ VF
M'L
L
1
W=LP 9 = C₁ q = W³P, 9 = Qin
q
드
E
VF
M'L
L

Transcribed Image Text:With these in mind, the approximation equations are written in brackets next to the governing
equations. The solution for the toughness dominated regime can be found from simultaneously
satisfying Elasticity, Continuity, Propagation, and the Inlet Boundary Condition, that is
K₁=PL¹2,
W =
â=
One path to the algebraic solution is as follows:
W
LP
E
W =
O..
L
LP
E
W
t
W ĝ
t L
W g
t
L'
Lin
à.. W
Lt Ľ²
K₁=PL¹/¹²,
LP LP Qi
E tE Ľ²
Q
= →W= ::
t Ľ
QEt
P= → K₁=PL¹² :: Ke
Ľ²³
K. - QK¹ - L-(K)
QiE't
=
[5/2
QEt
LP
L₁, P₁ →W=W=
E
2
= ⇒P=
2/5
QEt
Ľ
â = Lin
QE't
Ľ
-L¹/2 =
QE't
LS/2
q=
2/5
QE't
L₁₂ =
⇒P=
- (CE₁) +P = OF ² = P = QE ( 2 E₁)" :-:-(5)
P =
QEt
Ľ
Et
EQt
K
1 K₁
EQEt EQ)
1/5
L
:.W₁ =
KQt
E'A
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps

Knowledge Booster
Similar questions
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

