
Calculus: Early Transcendentals
8th Edition
ISBN: 9781285741550
Author: James Stewart
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Question
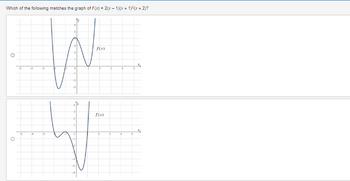
Transcribed Image Text:### Analyzing Polynomial Graphs
**Question:**
Which of the following matches the graph of \( f(x) = 2(x - 1)(x + 1)^2(x + 2)? \)
**Explanation:**
We start by analyzing the given polynomial function \( f(x) = 2(x - 1)(x + 1)^2(x + 2) \). The degrees of the polynomial and the roots can be identified to understand the possible shape of the graph.
- The roots are \(x = 1\), \(x = -1\) (which is a double root), and \(x = -2\).
- At \(x = 1\): The graph will cross the x-axis.
- At \(x = -1\): The graph will touch the x-axis and turn around since \(x = -1\) is a double root.
- At \(x = -2\): The graph will cross the x-axis.
### Graph 1:
**Description:**
The graph shows a polynomial curve with the following characteristics:
- Crosses the x-axis at \(x = 1\) and \(x = -2\).
- Touches the x-axis at \(x = -1\) and turns back up, indicating a double root.
- The graph follows a consistent end behavior as \( x \to -\infty \) and \(x \to +\infty\).
### Graph 2:
**Description:**
This graph showcases a different polynomial curve:
- Crosses the x-axis at multiple points.
- The behavior at the roots isn't consistent with a double root at \(x = -1\), as it doesn't solely touch and turn at this point.
### Detailed Analysis:
The correct graph should:
- Cross the x-axis at \(x = 1\) and \(x = -2\).
- Touch and turn at \(x = -1\) indicating a double root at this point.
### Conclusion:
**Graph 1** accurately represents the graph of \(f(x) = 2(x - 1)(x + 1)^2(x + 2)\). It correctly displays the polynomial touching and turning at \(x = -1\) (double root), and crossing at \(x = 1\) and \(x = -2\).
### Additional Notes:
- Understanding the nature of roots and their multiplicities is crucial for sketching polynomial
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 3 steps with 8 images

Knowledge Booster
Similar questions
- Find a symbolic representation for f-1(x) f(x)=6x3+3arrow_forwardFind the following. x2 x2 + 1 f(x) = Vx2 - 4, g(x) = (a) (f+ g)(x) = (b) (f - g)(x) = %3D (c) (fg)(x) = %3D (d) (f/g)(x) = What is the domain of f/g? (Enter your answer using Interval notation.)arrow_forwardFind the domain of f(x) x+1 / x2-6x+5arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning

Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning