
Algebra and Trigonometry (6th Edition)
6th Edition
ISBN: 9780134463216
Author: Robert F. Blitzer
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Question
Which graph represents the solution of y >= x ^ 2 + 2 ?
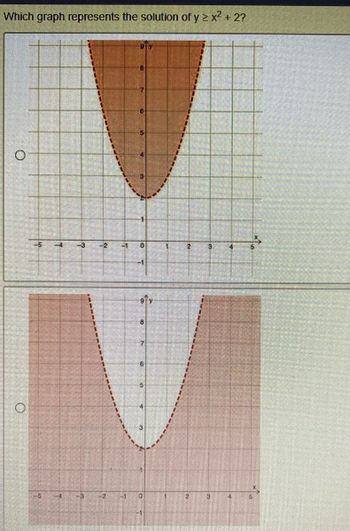
Transcribed Image Text:**Which graph represents the solution of y ≥ x² + 2?**
This image shows two graphs, both illustrating a parabola and shaded regions, with the aim to determine which graph accurately represents the solution for the inequality \( y \ge x^2 + 2 \).
### First Graph:
- **Parabola:** The parabola represented by the equation \( y = x^2 + 2 \) is depicted with a dashed red line.
- **Shaded Region:** The region above the parabola (where \( y \ge x^2 + 2 \)) is shaded in a solid brown color.
- **Axes:** The graph has horizontal and vertical axes, with the horizontal axis (x-axis) ranging from -5 to 5, and the vertical axis (y-axis) ranging from 0 to 9.
### Second Graph:
- **Parabola:** Similar to the first graph, the parabola is represented by the equation \( y = x^2 + 2 \) and is outlined with a dashed red line.
- **Shaded Region:** Contrary to the correct representation, the shaded region here is below the parabola, in a solid brown color.
- **Axes:** This graph also features horizontal and vertical axes, with the x-axis ranging from -5 to 5, and the y-axis from 0 to 9.
### Explanation:
For the inequality \( y \ge x^2 + 2 \), the solution includes all points on and above the parabola \( y = x^2 + 2 \). Thus, the correct representation is the one where the region above the curve is shaded.
**Correct Graph:**
The first graph accurately represents the solution for \( y \ge x^2 + 2 \), as the area above the curve (including the curve itself) is shaded.
Transcribed Image Text:### Understanding Graphs of Quadratic Functions
Quadratic functions, which are polynomial functions of degree 2, can be represented graphically by parabolas. Here, we analyze the graphs of two quadratic functions shown in the images.
#### First Graph:
- **Axes**: The horizontal axis is labeled x, and the vertical axis is labeled y. Both axes are marked with increments.
- **Graph Description**: The parabola opens upwards, signifying that the coefficient of the quadratic term is positive. The vertex of the parabola, which is the minimum point, appears to be at (0, 3). The graph is shaded in red from the vertex upwards.
Key Characteristics:
- **Vertex**: (0, 3)
- **Direction**: Upward
- **X-Intercepts**: The graph does not cross the x-axis, implying complex roots or no real roots.
- **Y-Intercept**: The graph crosses the y-axis at (0, 3).
This indicates that the quadratic function may have the general form of \( y = ax^2 + bx + c \) where the vertex form is \( y = a(x-h)^2 + k \) and here \( h = 0, k = 3 \).
#### Second Graph:
- **Axes**: Similar to the first graph, the horizontal axis is labeled x, and the vertical axis is labeled y. Both axes are marked with increments.
- **Graph Description**: The parabola in this graph opens downwards, indicating that the coefficient of the quadratic term is negative. The vertex of the parabola is at (0, 3). The graph is shaded in red from the vertex downwards.
Key Characteristics:
- **Vertex**: (0, 3)
- **Direction**: Downward
- **X-Intercepts**: The graph does not cross the x-axis, implying no real roots or complex roots.
- **Y-Intercept**: The graph crosses the y-axis at (0, 3).
This signifies that the quadratic function is likely in the form \( y = -ax^2 + bx + c \) where the vertex form is \( y = -a(x-h)^2 + k \) and, similarly, \( h = 0, k = 3 \).
### Summary:
Both graphs illustrate key properties of quadratic functions through their graphical representations:
1. **Vertex**: The turning point of the
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Similar questions
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON
Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning
Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON
Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press
Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education
College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education

Algebra and Trigonometry (6th Edition)
Algebra
ISBN:9780134463216
Author:Robert F. Blitzer
Publisher:PEARSON

Contemporary Abstract Algebra
Algebra
ISBN:9781305657960
Author:Joseph Gallian
Publisher:Cengage Learning

Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning

Algebra And Trigonometry (11th Edition)
Algebra
ISBN:9780135163078
Author:Michael Sullivan
Publisher:PEARSON

Introduction to Linear Algebra, Fifth Edition
Algebra
ISBN:9780980232776
Author:Gilbert Strang
Publisher:Wellesley-Cambridge Press

College Algebra (Collegiate Math)
Algebra
ISBN:9780077836344
Author:Julie Miller, Donna Gerken
Publisher:McGraw-Hill Education