
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
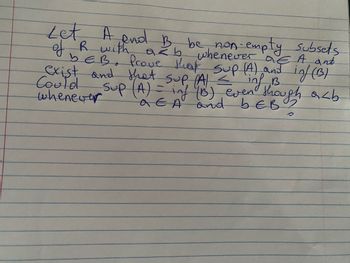
Transcribed Image Text:whenever a E A and
Let A and B be non-empty subsets
of R with azb
bEB. Prove that sup (A) and inf (1B)
exist and that sup (A) <
Could
whenever
inf B
Sup (A) = inf (B) even though arb
AEA and bEB
Expert Solution
arrow_forward
Step 1: Existence

Step by stepSolved in 3 steps with 3 images

Knowledge Booster
Similar questions
- Show that the following two wffs are not equivalent by writing down an interpretation with domainD = {a, b} that makes one wff true and the other wff false. Explain why one wff is true and theother is false with respect to your interpretation.∃x (p(x) ∧ q(x))and∃x p(x) ∧ ∃x q(x)arrow_forwardIs it true that, if S is a nonempty set of positive real numbers, then 0<=inf S?arrow_forwardthe follow Find the closure of each of the following sets: et og ned (a) (3,5) U {6} (b) (-∞, 0) U (0, 1)arrow_forward
- Let A, B, C be arbitrary finite sets from the same universal set U. - - (a) Is it true that A - B C (A - B) – (B − C)? If "yes", then prove "rigorously"; if "no", then show a concrete counterexample by specifying sets A, B, C where this subset relation does not hold. (To prove an expression of the form MCN "rigorously", you need to consider an arbitrary element x from M and show that x E N.) (b) Is it true that (A - B = A - C) → (B = C)? If "yes", then prove "rigorously"; if "no", then show a concrete counterexample by specifying sets A, B, C where this implication does not hold.arrow_forwardWithout proving anything, determine if the following statements are true or false. For any false statements, give an counterexample. (a) A finite, nonempty set of real numbers always contains its supremum. (b) If a < L for every element a in the set A, then sup A < L. (c) If A and B are sets with the property that a < b for every a E A and b e B, then sup A < inf B. (d) If sup A = s and sup B = t, then sup(A+ B) = s+t. Here and elsewhere, the set A+B is defined as A+B = {a+b:a € A, and b e B}. (e) If sup A < sup B then there is an element of B that is an upper bound for A.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

