Question
thumb_up100%
Consider a particle in the one-dimensional box with the following wave function: psi(x, 0) = Cx(a−x)
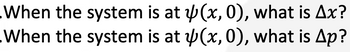
Transcribed Image Text:When the system is at
When the system is at
(x, 0), what is Ax?
(x, 0), what is Ap?
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 6 steps with 6 images

Knowledge Booster
Similar questions
- An electron is trapped in an infinitely deep one-dimensional well of width 0,251 nm. Initially the electron occupies the n=4 state. Find the energies of other photons that might be emitted if the electron takes other paths between the n=4 state and the ground statearrow_forwardSolve the time-independent Schrödinger equation and determine the energy levels and the wave function of a particle in the potential a? V (x) = Vol a + 2r2 with a = const.arrow_forwardShow that the hydrogen wave function Ψ211 is normalizedarrow_forward
- Particle of mass m moves in a three-dimensional box with edge lengths L1, L2, and L3. (a) Find the energies of the six lowest states if L1 =L, L2 = 2L, and L3 = 2L. (b) Which if these energies are degenerate?arrow_forwardShow that normalizing the particle-in-a-box wave function ψ_n (x)=A sin(nπx/L) gives A=√(2/L).arrow_forward
arrow_back_ios
arrow_forward_ios