
Elementary Geometry For College Students, 7e
7th Edition
ISBN: 9781337614085
Author: Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher: Cengage,
expand_more
expand_more
format_list_bulleted
Concept explainers
Topic Video
Question
number 33 only (9.1)
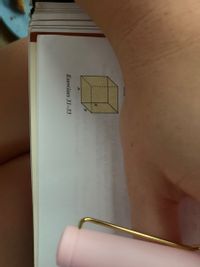
Transcribed Image Text:**Exercises 31-33**
The image appears to show a three-dimensional geometric figure, specifically a cube. The cube has several of its edges labeled as follows:
- Vertex A is identified at the top front-left corner of the cube.
- Vertex B is identified at the bottom front-left corner.
- Vertex C is identified at the bottom front-right corner.
- Vertex D is identified at the top back-left corner.
The cube is drawn with dashed lines representing the edges that are not visible from the current perspective, indicating a three-dimensional object.

Transcribed Image Text:### Mathematics Exercises
**32.** Use the formulas and drawings in Exercise 31 to find (a) the total area and (b) the volume of a cube with edges of length 5.3 ft each.
---
**33.** When the length of each edge of a cube is increased by 1 cm, the volume is increased by 61 cm³. What is the length of each edge of the original cube?
---
**34.** The numerical value of the volume of a cube equals the numerical value of its total surface area. What is the length of each edge of the cube?
---
**35.** The sum of the lengths of all edges of a cube is 60 cm. Find the volume \( V \) and the surface area \( S \) of the cube.
---
**36.** A concrete pad 4 in. thick is to have a length of 36 ft and a width of 30 ft. How many cubic yards of concrete must be poured?
---
These exercises are designed to help students apply mathematical formulas related to the properties of cubes in practical contexts. Students will practice calculating total area, volume, and relationships between the dimensions of cubes, reinforcing their understanding of geometry and measurement.
**Note:** For Exercise 32, refer to Exercise 31 for specific formulas and drawing references which are necessary to solve the problem.
**Graph/Diagram Explanation:**
While the problem set currently does not include any graphs or diagrams, it is important for students to visualize geometric problems. Diagrams showing cubes and their properties, such as edge length, volume, and surface area, can greatly aid in understanding.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, geometry and related others by exploring similar questions and additional content below.Similar questions
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning

Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,

Elementary Geometry for College Students
Geometry
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Cengage Learning