need chemistry review help 4NO₂ (g) + O₂(g) = 2N₂0, (8)Using the chemical equation you can write the pressure equilibrium constant expression equation:InitialNow comes the challenge. How are we going to find the equilibrium pressures to put into the right-hand side of this equation? One important clue is that you'retold the initial pressures. That suggests solving an equilibrium composition problem might be part of the solution. Let's go down that path a little and see whathappens.To solve for the equilibrium composition, you'd begin by setting up an ICE table. So let's do that. We'll let stand for the rise in pressure of the NO:ChangeN₂0₂NO₂EquilibriumPoJay₂0₂pV=nRTn= PVRTPK =P4.0-2xThe problem, of course, is that we don't know X, and we can't solve for it without.it. Are we stuck? Not necessarily. Let's think a moment about why knowingwould let us solve for X: it's because knowing that number gives us a relationship between the expressions in the "equilibrium" row of the ICE table. That is,we're able to combine these expressions into an equation with just one unknown, the value of X. An equation with just one unknown can always be solved forthe value of the unknown using algebra.NO₂4.0-2xIs there any other relationship we can imagine between the entries in the ICE table? Some other way to get an equation involving X?Maybe. The one other fact you're given is the mole fraction of N₂O, at equilibrium. That is, you're told the ratio of the moles of N₂O, to the total moles ofreactants and products. That's almost a relationship between the entries in the ICE table, except that it's in terms of moles. What we need is some way totransform it into a relationship between pressures.RTPN₂0₂PIOTWhen the issue is put like that, hopefully the idea of the ideal gas law comes to mind, because you know the ideal gas law relates pressure and moles for gases.Let's use the ideal gas law to figure out what relationship there is between the equilibrium pressure of N₂O, and the total pressure, given that we know therelationship between the moles of N₂O, and total moles:Px₂0₂RTPIOTPIOTP9.11-3x9.1-xPPos0Here's the ideal gas law.Solving for tells us how moles can be expressed in terms of pressure.Now we're getting somewhere. You're told ₂0₂² =0.11. That means you now know a relationship between the equilibrium pressure of N₂O, and the totalpressure. And that's all you need to solve for X, using the entries in the "equilibrium" row of the ICE table:Here's the definition of the mole fraction of N₂O₂.Here's what happens when we substitute in the ideal gas law expression for moles, top and bottom.You can solve this equation for X using algebra:x=0.11 (13.1-x)1.165x-1.441=0x= 1.237...Everything cancels but the pressures!(4.0-2x)-(9.1-x)+(x)Clear fractions.Multiply everything out.Solve the linear equation.The hard part is over. Now you just need to substitute this value for X back into the expressions in the "equilibrium" line of the ICE table, to get the equilibriumpressures. 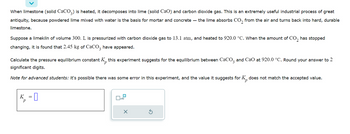These then go into the pressure equilibrium expression equation to give you13.1-x= 0.11x²(1.237)(4.0-23)*(91-3) (4.0-2(1.237))*(9.1-(1.237))= 0.03327...21ArH When limestone (solid CaCO3) is heated, it decomposes into lime (solid CaO) and carbon dioxide gas. This is an extremely useful industrial process of greatantiquity, because powdered lime mixed with water is the basis for mortar and concrete - the lime absorbs CO₂ from the air and turns back into hard, durablelimestone.Suppose a limekiln of volume 300. L is pressurized with carbon dioxide gas to 13.1 atm, and heated to 920.0 °C. When the amount of CO₂ has stoppedchanging, it is found that 2.45 kg of CaCO3 have appeared.Calculate the pressure equilibrium constant K this experiment suggests for the equilibrium between CaCO3 and CaO at 920.0 °C. Round your answer to 2significant digits.Note for advanced students: it's possible there was some error in this experiment, and the value it suggests for K does not match the accepted value.K =P0x10X

Mass of CaCO3 dissolved = 2.45 kg = 2450 g PCO2 = 13.1 atm T = 920 oC = 1193.15 K V = 300 L

Answered: When limestone (solid CaCO3) is heated,…

10th Edition

ISBN:9781305957404

Author:Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCoste

Publisher:Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCoste

Chapter1: Chemical Foundations

Section: Chapter Questions

Problem 1RQ: Define and explain the differences between the following terms. a. law and theory b. theory and...