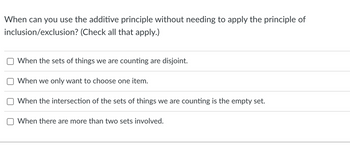
When can you use the additive principle without needing to apply the principle of inclusion/exclusion? (Check all that apply.)

Number of ChildrenTable 1 shows the number of women (per 1000) between 15 and 50 years of age who have been married grouped by the number of children they have had. Table 2 gives the same information for women who have never been married.1 Number of Children     Women per 1000 0   162 1   213 2   344 3   182 4   69 5+      32 Table 1 Women who have been married Number of Children     Women per 1000 0   752 1   117 2   72 3   35 4   15 5+      10 Table 2 Women who have never been married 1http://www.census.gov/hhes/fertility/data/cps/2014.html, Table 1, June 2014.   Condition gt requires numbers instead of "null" and "0" (a) Without doing any calculations, which of the two samples appears to have the highest mean number of children?  Women who have been marriedWomen who have never been married Which of the distributions appears to have the mean most different from the median?  Women who have been marriedWomen who have never been married…

what is n?

what is a sigma algebra?

What is the mathematical definition of a transposition?