Question
1- What is the value of alpha at state A when it calls min_value(D, alpha=?, beta=?). Enter -1000 for -Infinity; 1000 for +Infinity.
??
2- How many nodes are in the game tree? (Include terminal states)
??
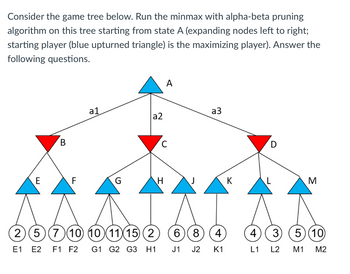
Transcribed Image Text:Consider the game tree below. Run the minmax with alpha-beta pruning
algorithm on this tree starting from state A (expanding nodes left to right;
starting player (blue upturned triangle) is the maximizing player). Answer the
following questions.
E
B
LL
F
A
al
a2
а3
C
G
H
K
2 5 7 10 10 11 15 (2)
E1 E2 F1 F2 G1 G2 G3 H1
(6)
D
M
68
4
4
3
5(10)
J1 J2
K1
L1
L2
M1
M2
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 3 steps

Knowledge Booster
Similar questions
- In what order are positions visited during a post-order traversal of the treedisplayed below? Label each node with the correct number Programming language: Java with outputarrow_forwardbool DelOddCopEven(Node* headPtr) { if (headPtr == nullptr) { return false; } Node* prev = nullptr; Node* current = headPtr; while (current != nullptr) { if (current->data % 2 != 0) { // Odd-valued node, delete it if (prev != nullptr) { prev->link = current->link; } else { headPtr = current->link; } Node* temp = current; current = current->link; delete temp; } else { // Even-valued node, create a copy and insert it after the original node Node* newNode = new Node; newNode->data = current->data; newNode->link = current->link; current->link = newNode; // Update the previous and current pointers prev = newNode; current = newNode->link; } } return true;} int FindListLength(Node* headPtr){ int length = 0;…arrow_forwardGiven the following premises: (1) ∀x (R(x) → S(x))(2) ¬S(c) Use modus tollens to derive the conclusion ¬R(c). Show your step-by-step reasoning.arrow_forward
- IN JAVA LANGUAGE ALL INFORMATION IN PICTURES FIND MIN OF A BST CALL ON A RECURSIVE FINDMIN_R THAT WILL RETURN THE SMALLEST ELEMENT IN A BST THANK YOU!!!!!!!!!!!arrow_forward*need correct answer plzarrow_forward12:34 A cs61a.org Implement add_d_leaves, a function that takes in a Tree instance t and a number v. We define the depth of a node in t to be the number of edges from the root to that node. The depth of root is therefore 0. For each node in the tree, you should add d leaves to it, where d is the depth of the node. Every added leaf should have a label of v. If the node at this depth has existing branches, you should add these leaves to the end of that list of branches. For example, you should be adding 1 leaf with label v to each node at depth 1, 2 leaves to each node at depth 2, and so on. Here is an example of a tree t (shown on the left) and the result after add_d_leaves is applied with v as 5. 3 2 3 2 4 4 5 5 5 Hint: Use a helper function to keep track of the depth! def add_d_leaves(t, v): """Add d leaves containing v to each ngarrow_forward
arrow_back_ios
arrow_forward_ios