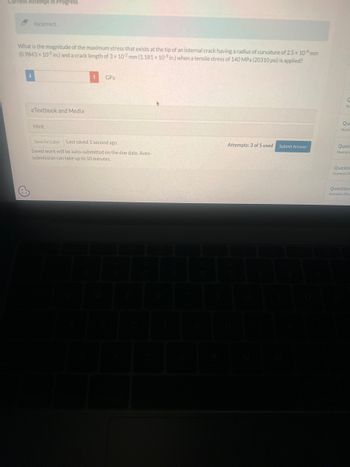
### Crack Tip Stress Calculation#### Problem StatementWhat is the magnitude of the maximum stress that exists at the tip of an internal crack having a radius of curvature of 2.5 × 10^-4 mm (0.9843 × 10^-5 in.) and a crack length of 3 × 10^-2 mm (1.181 × 10^-3 in.) when a tensile stress of 140 MPa (20310 psi) is applied?#### Answer Input- Input field for the answer in units of GPa. #### Interactive Elements- **Hint Section**: - Users can click to "Save for Later". - The saved work is last saved 1 second ago. - Information that saved work will be auto-submitted on the due date and that the auto-submission can take up to 10 minutes.- **Attempt Counter**: - Indicates "Attempts: 3 of 5 used". - Button to "Submit Answer".#### Additional Resources- eTextbook and Media section available but not expanded in the image.##### NoteThis page is an example of an educational question that involves the application of fracture mechanics concepts to calculate the stress at the tip of an internal crack under tensile loading. #### Visual Explanation- No graphs or diagrams are included in the provided image.This educational tool helps students understand the critical variables and calculation methods involved in materials science and mechanical engineering contexts, specifically related to fracture and stress analysis.

What is the magnitude of the maximum stress that exists at the tip of an internal crack having a radius of curvature of 2.5 x 10 mm (0.9843x 105 in.) and a crack length of 3x 102 mm (1.181 x 103 in.) when a tensile stress of 140 MPa (20310 psi) is applied? GPa

What is the magnitude of the maximum stress that exists at the tip of an internal crack having a radius of curvature of 2.5 x 10 mm (0.9843x 105 in.) and a crack length of 3x 102 mm (1.181 x 103 in.) when a tensile stress of 140 MPa (20310 psi) is applied? GPa

College Physics

11th Edition

ISBN:9781305952300

Author:Raymond A. Serway, Chris Vuille

Publisher:Raymond A. Serway, Chris Vuille

Chapter1: Units, Trigonometry. And Vectors

Section: Chapter Questions

Problem 1CQ: Estimate the order of magnitude of the length, in meters, of each of the following; (a) a mouse, (b)...

See similar textbooks

Similar questions

1 iron 40 cm steel 70 cm Henry has a rod that is made out of 2 parts. An iron and steel section. The iron section is 40cm long (Y₁=9.1 x 10¹⁰ N/m²). The iron piece is attached to a steel piece that is 70 cm long (Y,=7.0 x 10¹0⁰ N/m²). The rod has a uniform cross sectional diameter of 3.40 cm. Determine the total compression (in mm)when henry uses a compressive force on the rod of magnitude F=6000N. Look at the image provided to get a better understanding.
A square flat plate of dimensions 1 m x 1 m is moving with a maximum speed , U causing a fully laminar motion of it inside air ( density :1,2 kg /m3 viscosity :1.5x10-5 m2 /s ) Determine the magnitude of Shearing Stress on the surface of the plate SS=? at plate's trailing edge.ANSWER:SS= 0,0317 Pa
Between AB there is a 20 cm aluminum wire that supports a mass of 490 g and between BC another bronze cable of length 10 cm that supports a mass of 245 g; where EAL = 0.2x10¹¹ Pa (Young's modulus) and EBr = 5x10¹¹ Pa; with equal cross sections S = 0.2 cm² determine what length reaches point C. A - B - C
A steel bar two inches in diameter and 20 feet long resists a tensile load of 50,000 pounds. What is the unit tensile stress in the bar? Hint: Stress-force/area 7,958 psi 12,500 psi 15,915 psi 25,000 psi
2
3. A copper wire LM is fused at one end, M to an iron wire MN as shown in figure below. M N F The copper wire has length 0.90 m and cross-section area 0.90 x10-6 m². The iron wire has length 1.40 m and cross-section area 1.30 x10-6 m². The compound wire is stretched and the total length increases by 0.01 m. Given Yıron = 2.10 ×1011 Pa and Give Ycopper = 1.30 ×1011 Pa. Determine a. the ratio of the extension of copper wire to the extension of iron wire, b. the extension of each wire, and c. the applied force to the compound wire. [1.5, 4.0 mm, 6.0 mm, 780 N]
1. Consider the brass alloy for which the stress-strain behavior is a cylindrical specimen of this material 10.0 mm in diameter and 101.6 mm long is pulled in tension with a force of 10,000 N. If modulus of elasticity is 85 GPa compute the specimen elongation
The plug has a diameter of 30 mm and fits within a rigid sleeve having an inner diameter of 32 mm. Both the plug and the sleeve are 50 mm long. The plug is made from a material for which E= 1 MPa, v=0.7. (Figure 1) Figure Part A Determine the axial pressure p that must be applied to the top of the plug to cause it to contact the sides of the sleeve. Express your answer to three significant figures and include appropriate units. HA P= Submit Part B Value 8 = Request Answer Also, how far must the plug be compressed downward in order to do this? Express your answer to three significant figures and include appropriate units. μÅ 3 Value Submit Provide Feedback Units Request Answer IWIC ? Units www. ?
Problem Solving... The cross-sectional area of the bar is 5 cm2. Use E= 70 GPa for aluminum, and E= 200 GPa for steel. Aluminum Steel Aluminum 80 kN 20 kN 30 kN 70 kN A 3 m -4 m- 5 m- - What is the elongation in segment AB (Aluminum)? * -7.8571 x10^-3 m O6.8571 x10^-3 m O -6.8571 x10^-3 m 7.8571 x10^-3 m
You hang a heavy ball with a mass of 40 kg from a silver rod 2.8 m long by 2.2 mm by 2.7 mm. You measure the stretch of the rod, and find that the rod stretched 0.002384 m. Using these experimental data, what value of Young's modulus do you get? Y = 7.75e11 X N/m2 The atomic mass of silver is 108 g/mole, and the density of silver is 10.5 g/cm3. Using this information along with the measured value of Young's modulus, calculate the speed of sound in silver. V = m/s
Suppose a piano tuner stretches a steel piano wire 5.5 mm. The wire was originally 0.825 mm in diameter, 1.27 m long, and has a Young's modulus of 2.10 × 1011 N/m2. l0 = 1.27 ml = 5.5 mmd = 0.825 mm Calculate the force a piano tuner applies to stretch the steel piano wire in Newtons. F =
PROBLEM 4 For the assembly shown ibelow, find the maximum value of P that will not exceed a stress in steel of 140 MPa, in aluminum of 90 MPa of in bronze of 100 MPa and a total deformation of 3.5 mm. A = 500 mm2 A = 400 mm? A = 200 mm? %3D 2P 4P P- STEEL ALUMINUM BRONZE E = 200 GPa E = 70 GPa L = 2.0 m E = 83 GPa L = 1.5 m L = 2.5 m