Question
(lagrangian mechanics-Ordinary differantial equations)
lagrangian formulation of dynamics
- what is the first part of the matrix? "Fill"
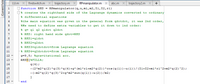
Transcribed Image Text:X trajectory.m x RPmanipulator.m x
RPmanipulator (q, u, ml, m2,I1,12,rl)
LU.m X
findswitch.m
abc.m
X trajectory2.m x +
1
function RHS =
* creates the righthand side of the Lagrange dynamics converted to ordinary
% differential equations
Sthe main equation was given in the general form qdotdot, it was 2nd order,
SWe need to define extra variables to get it down to Ind order:
$ q= ql q2 qldot q2dot
* RHS: right hand side qdot=RHS
* RHS1=qldot
* RHS2-q2dot
* RHS3=qldotdot=from Lagrange equation
* RHS4=q2dotdot=from Lagrange equation
2
3
4
7
8
10
11
12 -
g=9.8; gravitational acc.
13 -
RHS=[$FILL%;
g (4) ;
- (2*m2 *q (2) *q (3) *q(4) +g* (ml*rl+m2*q(2)) *cos (g (1)) -u (1) )/ (Il+12+ml*rl^2+m2*q(2) ^2);
14
15
16
- (-m2*g (2) *a(3) ^2+g*m2*sin (q (1))-u (2))/m2;
17
18 -
end
Current Fold
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps

Knowledge Booster
Similar questions
- 1arrow_forwardBook: Classical Dynamics of Particles and Systems Topic: Calculus of Variations Please answer in a detailed solution. For study purposes. Thank you.arrow_forwardDescribe the similarities and differences between the three equivalent ways of representing a system using classical mechanicsarrow_forward
- Derive using the Lagrangian and Lagrange's equation only. Please draw a diagramarrow_forwardDetermine the general solution of the 1-dimensional Laplace equation on the cylinder coordinates and ball coordinates!arrow_forward. Obtain the Euler – Lagrange equation for the extremals of the functional X2 | [y2 - yy'+y'2 ]dlx X1arrow_forward
- Introduction to Classical Dynamics The Lagrangian Method Please I need a complete solution of this, thank you.arrow_forwardThe Hamiltonian for the one dimensional quantum oscillator is 1 p² 1 Ĥ = 1² + ½ k²² = 12 + √ mw² ಠ2m 2m 2 where k = mw². 1) Define the operators ₁₁ and ₁₁ such that Ĥ = ½ħw (p² + ²). Define Ĥ2 as a function of 1 and p₁ such that Ĥ = hwĤ₂. - 2) Let us define the new operators â (1 + i₁) and ↠= ½(î₁ — ip₁). Express ₁ and p₁ as a function of â and â³. Knowing that [^^1,î₁] = i and [1, 1] = -i, calculate âât and â†â. Express Ĥ2 as a function of a and at. 3) Let us define Ñ such that Ĥ₂ = Ñ + ½. Knowing that Ĥ, Ĥ₂ and Ñ have the same eigenstates, what are their corresponding eigenvalues?arrow_forwardProblem 2 The relativistic Lagrangian for a particle of rest mass m moving along the x-axis in a potential V(x) is given by 2 L = -mc² 1 V(x) c2 (a) Derive the Euler-Lagrange equation of motion. (b) Show that it reduces to Newton's equation in the limit |*| << c. (c) Compute the Hamiltonian H of the system. Eliminate ȧ from the Hamiltonian by using the equation ƏL p = ax and write H = H(p, x) as a function of x and p only.arrow_forward
- 4. The Lagrangian of a relativistic particle is given by v2 L = -moc² 1- where mo is the rest mass of the particle, v is its velocity, and V is not velocity dependent. Find the generalized momentum and the Hamiltonian H. It may be shown that the relativistic kinetic energy T is -moc² (1-2) - V. Check that H = T + V.arrow_forwardThis is question 8.8 in John R. Taylor's "Classical Mechanics" textbook by the way! (ISBN: 9781891389221)arrow_forwardplease solvearrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios