
Elementary Geometry For College Students, 7e
7th Edition
ISBN: 9781337614085
Author: Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher: Cengage,
expand_more
expand_more
format_list_bulleted
Question

Transcribed Image Text:**Reflection of Coordinates Over x = -1**
In this exercise, you are asked to determine the coordinates of a shape after it is reflected over the line x = -1. Below is a diagram and the task at hand:
**Diagram Explanation:**
- A purple polygon with vertices labeled A, B, C, and D is plotted on a coordinate plane.
- The vertices of the preimage are given as:
- A (5, 4)
- B (3, 2)
- C (1, 1)
- D (-1, -3)
**Task:**
Reflect each point over the vertical line x = -1 and provide the new coordinates:
- A' (reflected coordinate)
- B' (reflected coordinate)
- C' (reflected coordinate)
- D' (reflected coordinate)
As a reminder, reflecting a point over a vertical line involves finding the horizontal distance from the point to the line of reflection and recreating the same distance on the opposite side.
Start by calculating the distance each original point is from the line x = -1, and use that to find each reflected point. Fill in the boxes with the new coordinates for A', B', C', and D'.
Expert Solution
arrow_forward
Step 1
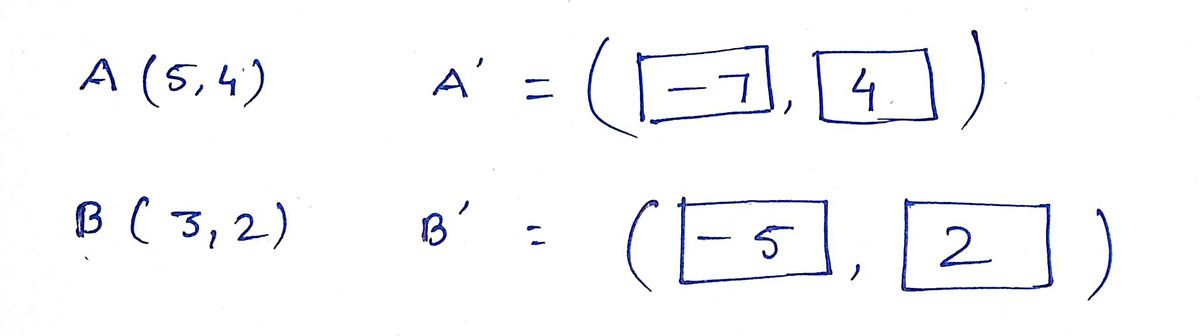
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Similar questions
Recommended textbooks for you
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning

Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,

Elementary Geometry for College Students
Geometry
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Cengage Learning