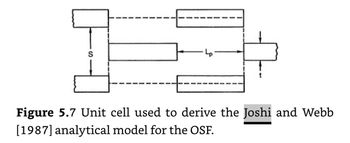
### Figure 5.7: Unit Cell for Derived Analytical ModelThe figure illustrates a unit cell that is utilized in deriving the analytical model by Joshi and Webb (1987) for the OSF (Orthogonally Stiffened Frame).#### Explanation:- **Unit Cell Structure:** The diagram shows a simplified representation of a unit cell.- **Arrows and Lines:** - Several arrows indicate forces or directions of stress/strain within the structure. - "S" denotes a specific parameter associated with the unit cell's structure. - "Lp" represents another parameter, possibly related to the length or another geometric aspect of the unit cell.### Detailed Description:- The unit cell consists of rectangular blocks with arrows suggesting the directions of forces or connections within the framework.- The outer rectangles are connected with dashed lines, likely indicating the boundary or the limits of the unit cell.- The parameter "S" and "Lp" are key variables in the model being derived.**Purpose:** This visual representation helps in understanding how the analytical model quantifies the behavior of the OSF by breaking it down into manageable units.**Reference:** Derived from the work of Joshi and Webb from their 1987 analytical model, the unit cell serves as a foundational element for studying and modeling structural behaviors in orthogonally stiffened frames.For more in-depth learning, refer to Joshi and Webb's original studies and subsequent elaborative content on analytical models for architectural and engineering frameworks. ### Application of Analytical Model for Heat Transfer and Friction Characteristics in OSF Arrays#### OverviewWe aim to implement the analytical model developed by Joshi and Webb to predict the heat transfer and friction characteristics (denoted as **j** and **f**, respectively) of the Offset Strip-Fin (OSF) array.#### Table 1: Surface Characteristics DataThe following table provides key parameters for two specific surface types used in the study.| **Surface** | **α** | **t/l** | **h (mm)** | **t (mm)** | **D_h (mm)** | **f** ||-------------|----------|---------|------------|------------|--------------|-----------|| 1 | 0.123 | 0.016 | 38.1 | 0.406 | 7.518 | 0.0551 || 8 | 0.224 | 0.064 | 38.1 | 1.626 | 10.897 | 0.0434 |#### Instructions1. **Plotting Nu vs fin length (l):** Use the Webb and Joshi model as specified in the course notes to create a plot of Nusselt number (Nu) versus the fin length (l) in the range of 1 mm to 5 mm, in 0.5 mm increments or smaller. For these calculations, utilize the following parameters: - α = 0.184 - t = 0.102 mm - h = 4.98 mm - \(Re_{D_h}\) = 500 While plotting, explain the behavior of the Nusselt number (Nu) in relation to different lengths (l). Assume the fin efficiency to be 1.2. **Conversion to j-factors:** Convert the Nusselt number data from Problem 2 into j-factors, assuming \(Pr = 0.7\). Next, calculate the friction factor for the same values of fin length (l), \(Re_{D_h}\), and the geometric parameters. Plot the ratio \(f/j\) versus the fin length (l) for the range 1 mm < l < 5 mm. Evaluate the plot to verify the Reynolds analogy and discuss why the observed trends should be expected.### Detailed Graphs and

We will answer the first question as you have not mentioned which would you like to be answered.…

We wish to use the analytical model developed by Joshi and Webb to predict the heat transfer and friction characteristics (j and f) of the Offset Strip-Fin (OSF) array. Surface 1 8 α 0.123 0.224 0.016 0.064 h (mm) 38.1 38.1 t (mm) 0.406 1.626 Dh (mm) 7.518 10.897 0.0551 0.0434

We wish to use the analytical model developed by Joshi and Webb to predict the heat transfer and friction characteristics (j and f) of the Offset Strip-Fin (OSF) array. Surface 1 8 α 0.123 0.224 0.016 0.064 h (mm) 38.1 38.1 t (mm) 0.406 1.626 Dh (mm) 7.518 10.897 0.0551 0.0434

Elements Of Electromagnetics

7th Edition

ISBN:9780190698614

Author:Sadiku, Matthew N. O.

Publisher:Sadiku, Matthew N. O.

ChapterMA: Math Assessment

Section: Chapter Questions

Problem 1.1MA

See similar textbooks

Similar questions

A steam pipe with outside diameter 10 mm, passes through a room, the surface temperature of the pipe is 100 °C and the air is at 25 °C. Convection coefficient is 15 W/ m2.K. The heat transfer from a tube of length 5 m is: Select one: a. 1767 W b. 1767 W/ m c. 1767 W /m2 d. 176 W e. 1765 W
Σ 00 6. B %24 https/0253A%252F%252Fnewconnect.mheducation.com%252F#/activity/question- CH-3) 6 Help Save & Exit i Required information A 14-cm × 20-cm circuit board houses on its surface 100 closely spaced logic chips, each dissipating 0.06 W in the environment at 40°C. The heat transfer from the back surface of the board is negligible. If the heat transfer coefficient on t1 of 3 the surface of the board is 10 W/m².K. Calculate the heat flux on the surface of the circuit board in terms of W/m (Round the final answer to two decimaj places.) Numeric Response Mc Graw < Prev 4. 11:35 18°C Partly sunny 9N3 ツゆ v 23/10/2021 tio SU 61 & 23 3 4. 5. н alt gr curi
Answer correctly and quickly as possible please.
R8
A sab 15 cm Later, one of the other surface temp is at 20°C initially, 100°C. and the increased to 50°C. profile in the slob ofter 3 min, using finste differences method. calculate the temp s += 15 min Dx = 5 cm 1.10 of m²/s The equation describing the system: d. 227 before 1 2 3 after 20°C 20°C 20°C 20°C 20°C 20°C 50°C +=0 100°C 20°C ? 50°C +=1₁5 105C ? 50°C + = 3 100°L ? of 2 thickness is surfaces is 2 maint oined increased to 0 Be 2x
A tube having a cylindrical shape of length equals to 30 m and diameter equals to 10 cm passes through a room. If the temperature of the outer surface of the tube is 110 C and the temperature of the air in the room is 10 C. Determine the rate of heat transfer by convection from the tube to the air. The heat transfer coefficient h = 3 W/m^2.K. Select one: a. 355 W b. 43 kW c. 2827.35 W
A J- type thermocouple is used to measure the temperature in a heating process. The length of the bare material is 120mm and thickness is 1.5mm. Find the time constant of the bare material. уре of Thermo-Material K ( Q W/m- (kg/m3) k) IS |(J/Kg- oc) couple J Iron- Constantan 46 8535 345 K Kromel- Alumel 35 8738 380 IT Copper- Constantan 160 8902 316 Cromel - Contantan 33 8825 336 Nicrocil- Nisil 34 8702 376 Pt(30%)Rhodium - 19 15718 56 Pt(6%)Rhodium Platinum(13%)Rodium, 55 16628 99 - Platinum Platinum(10%)Rodium 52.9 16745 99 Platinum Time constant of the bare material is, T=
Please solve correctly, will provide helpful ratings for correct solution.
1 33 2 30 6 7 8 9 13 14 17 19 20 21 22 230 11 43 24 25 34 26 38 390 400 41 42 44 45 46 49 QUESTION 1 A domestic refrigerator with inner dimensions of 0.7 m by 0.7 m at the base and height 1 m was designed to maintain a set temperature of 6 °C. The bodies consist of two 10-mm-thick layers of Aluminium (k = 225 W/mK) separated by a 30 mm polyurethane insulation (k-0.028 W/mK). If the average convection heat transfer coefficient at the inner and outer surfaces are 116 W/m²K and 14.5 W/m2K respectively, calculate the resistance(R) for the inner fluid thermal layer in K/W to 4 decimal places. 4 QUESTION 2 4 350 36 5 37 15 16 B