w²/4 |(−z|y(t))|² = = (wow)² + w/4 sin² - (wow)² + w/4 2
Comparisons of the energy differences between two states with that predicted by theory can test the theoretical model. For the case of the muon g-value, there's a small discrepancy between it and the Standard Model of particle physics. We can see atomic transitions in cesium in atomic clocks. We can measure the frequency by applying pulses at frequencies to observe the resonance (see the provided equation, Rabi's formula).
Consider a spin-1/2 particle that precesses in a magnetic field in the z direction. The probability of the particle being spin up or spin down along z doesn’t vary with time. The states |+z> and |—z> are stationary states of the Hamiltonian H-hat = ω0 S-hatz. If we alter the Hamiltonian by applying in addition an oscillating magnetic field transverse to the z axis, we can induce transitions between these two states by properly adjusting the frequency of this transverse field. The energy difference E+—E_ = h-bar ω0 can then be measured with high accuracy. This magnetic resonance gives us an excellent way of determining ω0. Initially, physicists used magnetic resonance techniques to make accurate determinations of g factors and thus gain fundamental information about the nature of these particles. On the other hand, with known values for g, one can use the technique to make accurate determinations of the magnetic field B0 in which the spin is processing. For electrons or nuclei in atoms or molecules, this magnetic field is a combination of the known externally applied field and the local magnetic field at the site of the electron or nucleus.
Question:
- If you start this spin-1/2 system in the spin-up and drive on-resonance, where ω = ω0, for a time Tπ, you'll end up spin-down. We call a drive of this length a pi-pulse. What is Tπ in terms of ω1 and/or ω0?
AI-generated content may present inaccurate or offensive content that does not represent bartleby’s views.
Unlock instant AI solutions
Tap the button
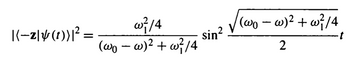
to generate a solution