• VP1. The object of mass m shown in th figure below is attached to a vertical roc by two strings of length e. The strings a attached to the rod at points a distance apart. The object rotates in a horizontal circle at a constant speed of v, and the ut Tho ro nas
• VP1. The object of mass m shown in th figure below is attached to a vertical roc by two strings of length e. The strings a attached to the rod at points a distance apart. The object rotates in a horizontal circle at a constant speed of v, and the ut Tho ro nas
Related questions
Question
New VP1
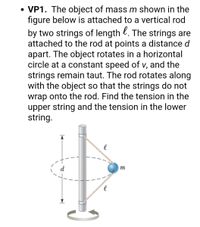
Transcribed Image Text:**VP1.** The object of mass \( m \) shown in the figure below is attached to a vertical rod by two strings of length \( \ell \). The strings are attached to the rod at points a distance \( d \) apart. The object rotates in a horizontal circle at a constant speed of \( v \), and the strings remain taut. The rod rotates along with the object so that the strings do not wrap onto the rod. Find the tension in the upper string and the tension in the lower string.
**Diagram Explanation:**
The diagram depicts a system where an object with mass \( m \) is suspended by two strings of equal length \( \ell \) attached to a vertical rod. These strings connect at two separate points on the rod, vertically separated by a distance \( d \). The object revolves in a horizontal plane around the rod, with the strings forming angles due to the object's circular motion. The setup suggests that tensions in the upper and lower strings need to be calculated, considering the system's dynamics.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by step
Solved in 4 steps with 1 images
