Question
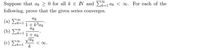
Transcribed Image Text:Suppose that ak > 0 for all k e N and E ak < 0. For each of the
following, prove that the given series converges.
ak
( a ) ΣΕΙ
1+ k3ak
(b) Lk=1 1+ ak
Vak
(c) Ek=1 k
< 0o.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 4 steps with 4 images

Knowledge Booster
Similar questions
- Show that the power law relationship P(Q) = kQr, for Q > 0 and r # 0, has an inverse that is also a power law, Q(P) = mP s, where m = k - l/r and s = 1/ r.arrow_forwardWhat is y(x) given that d²y dx² +4e-2x = 0 where you have the boundary conditions: dy dx y = yo (a constant) at You have to integrate twice as this is a second order differential equation so you need two boundary conditions to get the complete solution. (Most people are better at differentiating then integrating so check your answer by differentiating it!) = q (a constant) at x = 0 x = 0arrow_forwardWhat is “fractional error” for the following formula? Z= 2/3 X2Y3 , X= 7m , Y= 4m, σx=0.2m , σy=0.1m σZ=?arrow_forward
- QUESTION 4 E sin () sin () sin () 3nx 2nz Consider the case of a 3-dimensional particle-in-a-box. Given: Y = 1.5 What is the size of the box along the x-dimension? 2 3 none are correctarrow_forwardNeeds Complete solution with 100 % accuracy. otherwise skip if u can't give complete solution...arrow_forwardThe interplanar spacing of (121) planes is 4.5Å for a cubic crystal. Find the atomic radius for a face-centred cubic close packed structure.arrow_forward
- compute the accepted value of garrow_forwardThe Taylor expansion of the function In(cosh x), where x is real, about the point x = 0 starts with the following terms: 1 4 (a) x² + X +.... (b) = x² - 1/2x¹² +.. 2 (c) (1) 1/1 + +... - + 1 6 + 6arrow_forwardPlease do not rely too much on chatgpt, because its answer may be wrong. Please consider it carefully and give your own answer. You can borrow ideas from gpt, but please do not believe its answer.Very very grateful!Please do not rely too much on chatgpt, because its answer may be wrong. Please consider it carefully and give your own answer. You can borrow ideas from gpt, but please do not believe its answer. Very very grateful!arrow_forward
arrow_back_ios
arrow_forward_ios